如图，在平面直角坐标系中，矩形OABC的边OA=2，OC=6，在OC上取点D将△AOD沿AD翻折，使O点落在AB边上的E点处，将一个足够大的直角三角板的顶点P从D点出发沿线段DA→AB移动，且一直角边始终经过点D，另一直角边所在直线与直线DE，BC分别交于点M，N．
（1）填空：D点坐标是（ ， ），E点坐标是（ ， ）；
（2）如图1，当点P在线段DA上移动时，是否存在这样的点M，使△CMN为等腰三角形？若存在，请求出M点坐标；若不存在，请说明理由；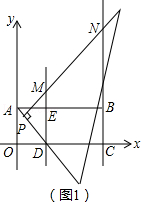
（3）如图2，当点P在线段AB上移动时，设P点坐标为（x，2），记△DBN的面积为S，请直接写出S与x之间的函数关系式，并求出S随x增大而减小时所对应的自变量x的取值范围．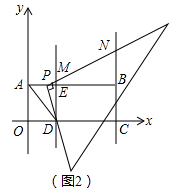
3-(+63)-(-259)-(-41)+（-40）
阅读下面例题的解答过程，体会并其方法，并借鉴例题的解法解方程。
例：解方程x2－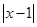
-1=0.
解：（1）当x－1≥0即x≥1时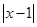，= x－1。
原化为方程x2－（x－1）-1=0，即x2－x=0
解得x1 =0．x2=1
∵x≥1，故x =0舍去，
∴x=1是原方程的解。
（2）当x－1＜0即x＜1时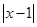，=－（x－1）。
原化为方程x2+（x－1）-1=0，即x2+x－2=0
解得x1 =1．x2=－2
∵x＜1，故x =1舍去，
∴x=－2是原方程的解。
综上所述，原方程的解为x1 =1．x2=－2
解方程x2－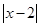
－4=0.
文峰服装超市在销售中发现：“宝乐”牌童装平均每天可售出20件，每件盈利40元。为了迎接“十·一”国庆节，商场决定采取适当的降价措施，扩大销售量，增加盈利，尽快减少库存。经市场调查发现：如果每件童装降价4元，那么平均每天就可多售出8件。要想平均每天在销售这种童装上盈利1200元，那么每件童装应降价多少？
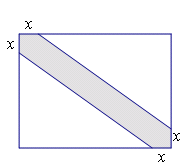
小明家有一块长8
，宽6的矩形空地，妈妈准备在该空地上建造一个花园，并使花园面积为空地面积的一半.小明设计了如下的四种方案供妈妈挑选.请你选择其中的一种方案帮助小明求出图中的
值.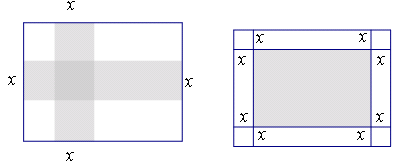
已知一元二次方程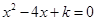
有两个不相等的实数根．
(1)求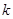
的取值范围；
(2)如果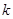是符合条件的最大整数，且一元二次方程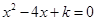与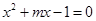
有一个相同的根，求此时
的值．