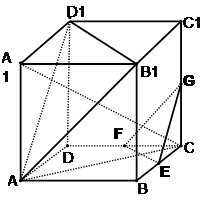已知函数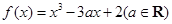 .
.
(Ⅰ)求函数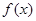 的单调递增区间;
的单调递增区间;
(Ⅱ)当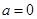 时,在曲线
时,在曲线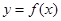 上是否存在两点
上是否存在两点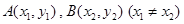 ,使得曲线在
,使得曲线在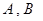 两点处的切线均与直线
两点处的切线均与直线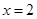 交于同一点?若存在,求出交点纵坐标的取值范围;若不存在,请说明理由;
交于同一点?若存在,求出交点纵坐标的取值范围;若不存在,请说明理由;
(Ⅲ)若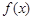 在区间
在区间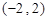 存在最大值
存在最大值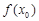 ,试构造一个函数
,试构造一个函数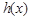 ,使得
,使得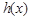 同时满足以下三个条件:①定义域
同时满足以下三个条件:①定义域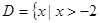 ,且
,且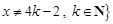 ;②当
;②当 时,
时,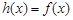 ;③在
;③在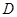 中使
中使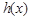 取得最大值
取得最大值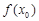 时的
时的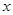 值,从小到大组成等差数列.(只要写出函数
值,从小到大组成等差数列.(只要写出函数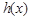 即可)
即可)
(本小题满分14分)
已知二次函数 的最小值为1,且
的最小值为1,且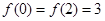 .
.
(1)求 的解析式;
的解析式;
(2)若 在区间
在区间 上不单调,求实数
上不单调,求实数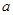 的取值范围;
的取值范围;
(3)在区间 上,
上,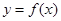 的图象恒在
的图象恒在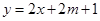 的图象上方,试确定实数
的图象上方,试确定实数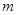 的取值范围.
的取值范围.
(本小题满分14分)
已知全集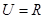 ,集合
,集合 ,
,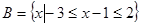 ,
,
(1)求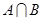 、
、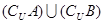 ;
;
(2)若集合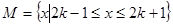 是集合
是集合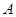 的子集,求实数
的子集,求实数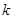 的取值范围.
的取值范围.
(本小题满分14分)
(1)化简: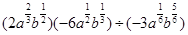 ;
;
(2)已知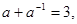 求
求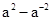 的值.
的值.
(本题15分)如图,AC 是圆 O 的直径,点 B 在圆 O 上,∠BAC=30°,BM⊥AC交 AC 于点 M,EA⊥平面ABC,FC//EA,AC=4,EA=3,FC=1.
(I)证明:EM⊥BF;
(II)求平面 BEF 与平面ABC 所成锐二面角的余弦值.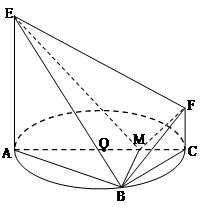
(本大题12分)如图,在棱长为ɑ的正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点.
(1)求直线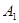 C与平面ABCD所成角的正弦的值;
C与平面ABCD所成角的正弦的值;
(2)求证:平面A B1D1∥平面EFG;
(3)求证:平面AA1C⊥面EFG .