某商品一年内出厂价格在6元的基础上按月份随正弦曲线波动,已知3月份达到最高价格8元,7月份价格最低为4元.该商品在商店内的销售价格在8元基础上按月份随正弦曲线波动,5月份销售价格最高为10元,9月份销售价最低为6元.
(1)试分别建立出厂价格、销售价格的模型,并分别求出函数解析式;
(2)假设商店每月购进这种商品m件,且当月销完,试写出该商品的月利润函数;
(3)求该商店月利润的最大值.(定义运算
(本小题满分14分)设椭圆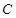 :
: 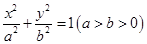 过点(0,4),离心率为
过点(0,4),离心率为 .
.
(1)求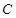 的方程;
的方程;
(2)求过点(3,0)且斜率为 的直线被
的直线被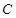 所截线段的中点坐标.
所截线段的中点坐标.
(本小题满分14分)如图,一简单几何体有五个顶点 、
、 、
、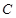 、
、 、
、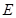 ,它的一个面
,它的一个面 内接于⊙
内接于⊙ ,
,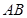 是⊙
是⊙ 的直径,四边形
的直径,四边形 为平行四边形,
为平行四边形,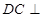 平面
平面 .
.
(1)证明:平面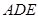
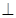 平面
平面 ;
;
(2)若 ,
,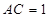 ,
,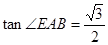 ,求该简单几何体的体积.
,求该简单几何体的体积.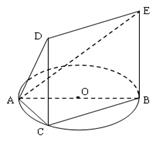
( 本小题满分14分)已知函数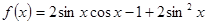
(1) 求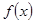 的最小正周期和最大值;
的最小正周期和最大值;
(2) 若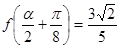 ,
,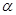 是第二象限的角,求
是第二象限的角,求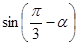 和
和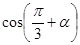 的值.
的值.
(本小题满分12分)为了分析某个高中学生的学习状态,对其下一阶段的学习提供指导性建议。现对他前7次考试的数学成绩 、物理成绩
、物理成绩 进行分析。下面是该生7次考试的成绩,可见该生的物理成绩
进行分析。下面是该生7次考试的成绩,可见该生的物理成绩 与数学成绩
与数学成绩 是线性相关的:
是线性相关的:
| 数学 |
88 |
83 |
117 |
92 |
108 |
100 |
112 |
| 物理 |
94 |
91 |
108 |
96 |
104 |
101 |
106 |
(1)求物理成绩 与数学成绩
与数学成绩 的回归直线方程
的回归直线方程 ;
;
(2)若该生的物理成绩达到115分,请你估计他的数学成绩大约是多少?
参考公式: ,
, 
参考数据: ,
,
(本小题满分12分)用分析法证明: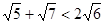 ;
;