某大学外语系有5名大学生参加南京青奥会翻译志愿者服务,每名大学生都随机分配到奥体中心体操和游泳两个比赛项目(每名大学生只参加一个项目的服务).
(1)求5名大学生中恰有2名被分配到体操项目的概率;
(2)设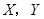 分别表示5名大学生分配到体操、游泳项目的人数,记
分别表示5名大学生分配到体操、游泳项目的人数,记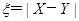 ,求随机变量
,求随机变量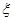 的分布列和数学期望
的分布列和数学期望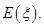
【2015高考安徽,理19】如图所示,在多面体 ,四边形
,四边形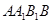 ,
, 均为正方形,
均为正方形, 为
为 的中点,过
的中点,过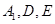 的平面交
的平面交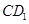 于F.
于F.
(Ⅰ)证明: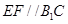 ;
;
(Ⅱ)求二面角 余弦值.
余弦值.
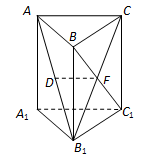
【2015江苏高考,16】如图,在直三棱柱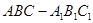 中,已知
中,已知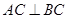 ,
,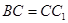 ,设
,设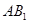 的中点为
的中点为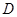 ,
,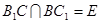 .
.
求证:(1)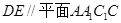 ;
;
(2)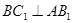 .
.
【2015高考新课标2,理19】
如图,长方体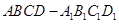 中,
中,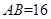 ,
, ,
,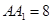 ,点
,点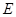 ,
,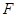 分别在
分别在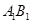 ,
,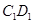 上,
上,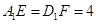 .过点
.过点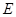 ,
,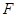 的平面
的平面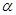 与此长方体的面相交,交线围成一个正方形.
与此长方体的面相交,交线围成一个正方形.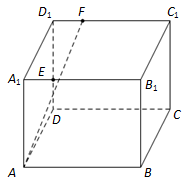
(Ⅰ)在图中画出这个正方形(不必说出画法和理由);
(Ⅱ)求直线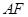 与平面
与平面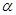 所成角的正弦值.
所成角的正弦值.
【2015高考上海,理21】已知椭圆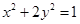 ,过原点的两条直线
,过原点的两条直线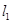 和
和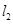 分别于椭圆交于
分别于椭圆交于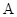 、
、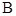 和
和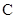 、
、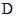 ,记得到的平行四边形
,记得到的平行四边形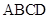 的面积为
的面积为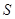 .
.
(1)设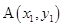 ,
,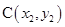 ,用
,用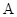 、
、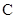 的坐标表示点
的坐标表示点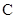 到直线
到直线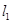 的距离,并证明
的距离,并证明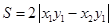 ;
;
(2)设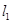 与
与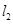 的斜率之积为
的斜率之积为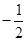 ,求面积
,求面积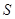 的值.
的值.
【2015高考湖南,理20】已知抛物线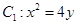 的焦点
的焦点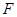 也是椭圆
也是椭圆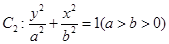 的一个焦点,
的一个焦点,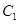 与
与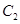 的公共弦的长为
的公共弦的长为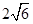 .
.
(1)求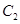 的方程;
的方程;
(2)过点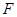 的直线
的直线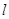 与
与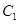 相交于
相交于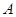 ,
,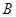 两点,与
两点,与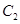 相交于
相交于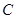 ,
,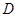 两点,且
两点,且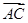 与
与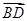 同向
同向
(ⅰ)若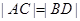 ,求直线
,求直线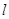 的斜率
的斜率
(ⅱ)设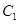 在点
在点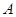 处的切线与
处的切线与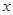 轴的交点为
轴的交点为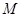 ,证明:直线
,证明:直线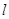 绕点
绕点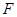 旋转时,
旋转时,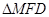 总是钝角三角形
总是钝角三角形