如图,在直三棱柱(即侧棱与底面垂直的三棱柱) 中,
中,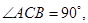
 ,
, 为
为 的中点
的中点
(I)求证:平面 平面
平面 ;
;
(II)求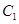 到平面
到平面 的距离.
的距离.
、已知直线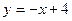 与曲线
与曲线 相交于
相交于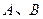 两点,若
两点,若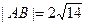 ,求
,求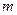 的值.
的值.
(I)若椭圆的焦点为 ,且经过点
,且经过点 ,求椭圆的标准方程.
,求椭圆的标准方程.
(II)求过点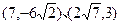 的双曲线的标准方程.
的双曲线的标准方程.
(本小题满分10分)
已知函数
 ,设关于
,设关于 的方程
的方程 的两实数根为
的两实数根为 ,
, 的两实根为
的两实根为 、
、 ,且
,且 .
.
(1)若 均为负整数,求
均为负整数,求 解析式;
解析式;
(2)若 ,求
,求 的取值范围.
的取值范围.
(本小题满分8分)
设蚂蚁在如图正方体的表面沿棱爬行,它从一个顶点爬向另外三个顶点是等可能的,若蚂蚁的初始位置在顶点A,回答下列问题: 
(1)若爬了两条线段(线段可以重复爬行),写出蚂蚁经过的所有路径;
(2)若爬了两条线段(线段可以重复爬行),蚂蚁停在顶点C的概率是多少?
(3)若爬了三条线段(线段可以重复爬行),蚂蚁停在顶点G的概率是多少?
(本小题满分8分)
某交易市场的土豆在30天内每吨的交易价 (千元)与时间
(千元)与时间 (天)(
(天)( ),组成有序数对
),组成有序数对 ,点
,点 落在如图所示的两条线段上,该市场土豆在30天内的日交易量
落在如图所示的两条线段上,该市场土豆在30天内的日交易量  (吨)与时间
(吨)与时间 (天)的部分数据如下表所示
(天)的部分数据如下表所示
第 天 天 |
4 |
10 |
16 |
22 |
 (吨) (吨) |
36 |
30 |
24 |
18 |

(1)根据提供的图象,写出每吨交易价格 (千元)与时间
(千元)与时间 (天)所满足函数关系式;
(天)所满足函数关系式;
(2)根据表中数据确定日交易量 (吨)与时间
(吨)与时间 (天)的一次函数解析式;
(天)的一次函数解析式;
(3)用 表示日交易额(千元),写出
表示日交易额(千元),写出 关于
关于 的函数解析式,问这30天中第几天交易额最大,最大值多少?
的函数解析式,问这30天中第几天交易额最大,最大值多少?