已知在 中,
中, 且三边长构成公差为2的等差数列,则
且三边长构成公差为2的等差数列,则 所对的边
所对的边 = .
= .
已知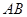 为半圆
为半圆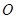 的直径,
的直径, ,
, 为半圆上一点,过点
为半圆上一点,过点 作半圆的切线
作半圆的切线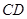 ,过点
,过点 作
作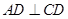 于
于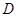 ,交圆于点
,交圆于点 ,
,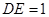 .
.
(Ⅰ)求证: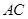 平分
平分 ;
;
(Ⅱ)求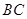 的长.
的长.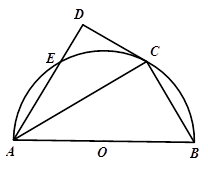
已知函数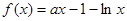
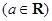 .
.
(Ⅰ)讨论函数 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(Ⅱ)若函数 在
在 处取得极值,对
处取得极值,对
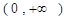 ,
, 恒成立,
恒成立,
求实数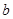 的取值范围;
的取值范围;
(Ⅲ)当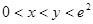 且
且 时,试比较
时,试比较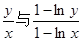 的大小.
的大小.
如图,已知抛物线 :
: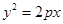 和⊙
和⊙ :
: ,过抛物线
,过抛物线 上一点
上一点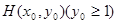 作两条直线与⊙
作两条直线与⊙ 相切于
相切于 、
、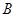 两点,分别交抛物线为E、F两点,圆心点
两点,分别交抛物线为E、F两点,圆心点 到抛物线准线的距离为
到抛物线准线的距离为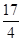 .
.
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)当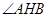 的角平分线垂直
的角平分线垂直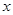 轴时,
轴时,
求直线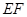 的斜率;
的斜率;
(Ⅲ)若直线 在
在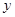 轴上的截距为
轴上的截距为 ,求
,求 的最小值.
的最小值.
已知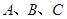 是
是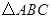 的三个内角,且满足
的三个内角,且满足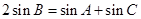 ,设
,设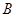 的最大值为
的最大值为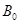 .
.
(Ⅰ)求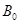 的大小;
的大小;
(Ⅱ)当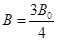 时,求
时,求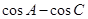 的值.
的值.
函数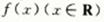 满足f(1)=1,且f(x)在R上的导函数
满足f(1)=1,且f(x)在R上的导函数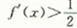 ,则不等式
,则不等式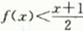 的解集为
的解集为