如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,﹣3)
(1)求此二次函数的解析式;
(2)在抛物线上存在一点P使△ABP的面积为10,请直接写出点P的坐标.
如图,在 ABCD的
ABCD的 各边AB、BC、CD、DA上,分别取点K、L、M、N,使A
各边AB、BC、CD、DA上,分别取点K、L、M、N,使A K=CM、BL=DN,求证:四边形KLMN为平行四边形。
K=CM、BL=DN,求证:四边形KLMN为平行四边形。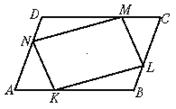
如图,要在一块形状为直角三角形(∠C为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮上画出一个半圆,使它的圆心在线段AC上,且与AB、BC都相切.请你用直尺和圆规画出来(要求用尺规作图,保留作图痕迹,不要求写作法).
计算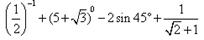
如图,在平面直角坐标系中,四边形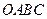 为矩形,
为矩形,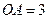 ,
,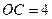 ,
,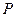 为直线
为直线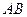 上一动点,将直线
上一动点,将直线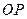 绕点
绕点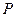 逆时针方向旋转
逆时针方向旋转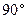 交直线
交直线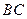 于点
于点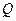 ;
;
(1)当点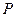 在线段
在线段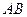 上运动(不与
上运动(不与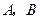 重合)时,求证:OA·BQ=AP·BP;
重合)时,求证:OA·BQ=AP·BP;
(2)在(1)成立的条件下,设点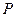 的横坐标为
的横坐标为 ,线段
,线段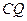 的长度为
的长度为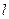 ,求出
,求出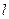 关于
关于 的函数解析式,并判断
的函数解析式,并判断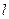 是否存在最小值,若存在,请求出最小值;若不存在,请说明理由。
是否存在最小值,若存在,请求出最小值;若不存在,请说明理由。
(3)直线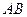 上是否存在点
上是否存在点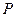 ,使
,使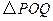 为等腰三角形,若存在,请求出点
为等腰三角形,若存在,请求出点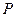 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
某电脑公司经销甲种型号电脑,今年三月份的电脑售价比去年同期每 台降价1000元,如果卖出相同数量的电脑,去年销售额为10万元,今年销售额只有8万元.
台降价1000元,如果卖出相同数量的电脑,去年销售额为10万元,今年销售额只有8万元.
(1)今年三月份甲种电脑 每台售价多少元?
每台售价多少元?
(2)为了增加收入,电脑公司决定再经销乙种型号电脑.已知甲种电脑每台进价为3500元,乙种电脑每台进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台,有几种进货方案?
(3) 如果乙种电脑每台售价为3800元,为打开乙种电脑的销路
如果乙种电脑每台售价为3800元,为打开乙种电脑的销路 ,公司决定每售出一台乙种电脑,返还顾客现金a元,要使(2)中所有方案获利相同,a值应是多少?
,公司决定每售出一台乙种电脑,返还顾客现金a元,要使(2)中所有方案获利相同,a值应是多少?