为了落实党中央提出的“惠民政策”,我市今年计划开发建设A、B两种户型的“廉租房”共40套.投入资金不超过200万元,又不低于198万元.开发建设办公室预算:一套A型“廉租房”的造价为5.2万元,一套B型“廉租房”的造价为4.8万元.
(1)请问有几种开发建设方案?
(2)哪种建设方案投入资金最少?最少资金是多少万元?
(3)在(2)的方案下,为了让更多的人享受到“惠民”政策,开发建设办公室决定通过缩小“廉租房”的面积来降低造价、节省资金.每套A户型“廉租房”的造价降低0.7万元,每套B户型“廉租房”的造价降低0.3万元,将节省下来的资金全部用于再次开发建设缩小面积后的“廉租房”,如果同时建设A、B两种户型,请你直接写出再次开发建设的方案.
已知直线y=x+6交x轴于点A,交y轴于点C,经过A和原点O的抛物线y=ax2+bx(a<0)的顶点B在直线AC上.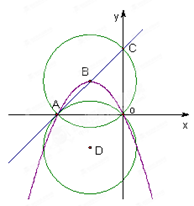
(1)求抛物线的函数关系式;
(2)以B点为圆心,以AB为半径作⊙B,将⊙B沿x轴翻折得到⊙D,试判断直线AC与⊙D的位置关系,并说明理由;
(3)若E为⊙B优弧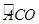 上一动点,连结AE、OE,问在抛物线上是否存在一点M,使∠MOA︰∠AEO=2︰3,若存在,试求出点M的坐标;若不存在,试说明理由.
上一动点,连结AE、OE,问在抛物线上是否存在一点M,使∠MOA︰∠AEO=2︰3,若存在,试求出点M的坐标;若不存在,试说明理由.
某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: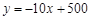 .
.
(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)
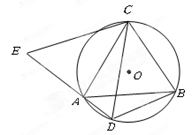
如图,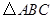 是
是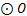 的内接三角形,
的内接三角形,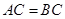 ,
,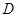 为
为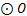 中
中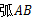 上一点,延长
上一点,延长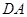 至点
至点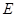 ,使
,使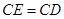 .
.
(1)求证: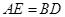 ;
;
(2)若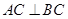 ,求证:
,求证: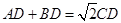 .
.
某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西30°方向,又航行了半小时到D处,望见灯塔C恰在西北方向,若船速为每小时20海里.
求A、D两点间的距离.
已知反比例函数y=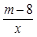 (m为常数)的图象经过点A(-1,6).
(m为常数)的图象经过点A(-1,6).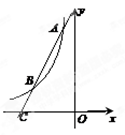
(1)求m的值;
(2)如图,过点A作直线AC与函数y=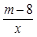 的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.