如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD= .
.
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.
如图,学校为美化校园,将形状是直角三角形的一园地△ABC,分别以三边AB、CA、BC为直径向外作半圆,开辟为三个花坛甲、乙、丙,现分给八年一班同学种花。班长准备让人数相等的两个小组同学负责。为了公平分配任务,她安排一个小组负责花坛甲,另一个小组负责花坛乙和丙。你认为班长的安排合理吗?请说明理由.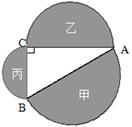
如图,在□ABCD中,AB=2 BC=4,点E、F分别是BC、AD的中点.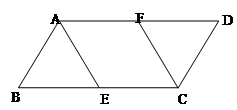
(1)求证:△ABE≌△CDF;
(2)当四边形AECF为菱形时,求出该菱形的面积.
已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点,△ABC
的顶点在格点上,称为格点三角形,试判断△ABC的形状.请说明理由.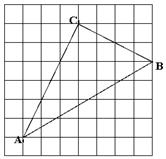
已知: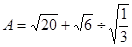 ,
, ,
,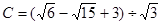 ,请你
,请你
从中选出你喜欢的两个字母,并求出它们的和.
如图,□ABCD的对角线AC,BD相交于点O,E,F分别是OA,OC的中点.
求证:BE=DF.