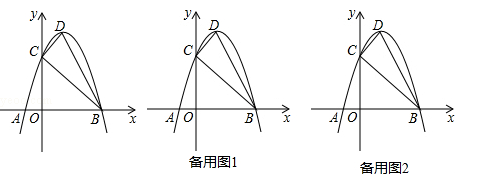
如图,抛物线y=ax2+c(a≠0)经过C(2,0),D(0,﹣1)两点,并与直线y=kx交于A、B两点,直线l过点E(0,﹣2)且平行于x轴,过A、B两点分别作直线l的垂线,垂足分别为点M、N.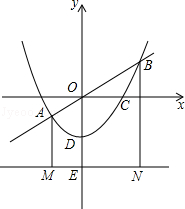
(1)求此抛物线的解析式;
(2)求证:AO=AM;
(3)探究:
①当k=0时,直线y=kx与x轴重合,求出此时 的值;
的值;
②试说明无论k取何值, 的值都等于同一个常数.
的值都等于同一个常数.
如图,在边长为1的小正方形网格中,三角形的三个顶点均落在格点上.
(1)以三角形的其中两边为边画一个平行四边形,并在顶点处标上字母A,B,C,D;
(2)证明四边形ABCD是平行四边形.
定义:底与腰的比是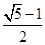 的等腰三角形叫做黄金等腰三角形.
的等腰三角形叫做黄金等腰三角形.
如图,已知△ABC中,AB=BC,∠C=36°,BA1平分∠ABC交AC于A1.
(1)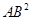 =AA1•A C;
=AA1•A C;
(2)探究:△ABC是否为黄金等腰三角形?请说明理由;(提示:此处不妨设AC=1)
(3)应用:已知AC=a,作A1B1∥AB交BC于B1,B1A2平分∠A1B1C交AC于A2,作A2B2∥AB交B2,B2A3平分∠A2B2C交AC于A3,作A3B3∥AB交BC于B3,…,依此规律操作下去,用含a,n的代数式表示An﹣1An.(n为大于1的整数,直接回答,不必说明理由)
定义:长宽比为 :1(n为正基数)的矩形称为株为
:1(n为正基数)的矩形称为株为 矩形.下面,我们通过折叠的方式折出一个
矩形.下面,我们通过折叠的方式折出一个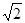 矩形.如图①所示.
矩形.如图①所示.
操作1:将正方形ABCD沿过点B的直线折叠,使折叠后的点C落在对角线BD上的点G处,折痕为BH
操作2:将AD沿过点G的直线折叠,使点A,点D分别落在边AB,CD上,折痕为EF
则四边形BCEF为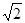 矩形
矩形
证明:设正方形ABCD的边长为1,则BD=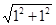 =
=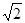 .
.
由折叠性质可知BG=BC=1,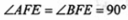 ,则四边形BCEF为矩形
,则四边形BCEF为矩形

阅读以上内容,回答下列问题:
在图 中,所有与CH相等的线段是 ,tan
中,所有与CH相等的线段是 ,tan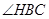 的值是
的值是
已知四边形BCEF为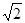 矩形,模仿上述操作,得到四边形BCMN,如图
矩形,模仿上述操作,得到四边形BCMN,如图 。
。
求证:四边形BCMN是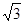 矩形
矩形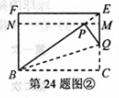
将图 中的
中的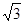 矩形BCMN沿用(2)中的操作3次后,得到一个“
矩形BCMN沿用(2)中的操作3次后,得到一个“ 矩形”,则n的值是
矩形”,则n的值是
在平面直角坐标系中,已知点A(-3,1),B(-2,0),C(0,1),请在图中画出△ABC,并画出与△ABC关于原点O对称的图形.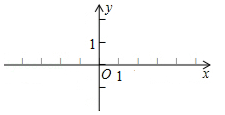
如图,抛物线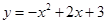 与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,请解决下列问题.
与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,请解决下列问题.
(1)填空:点C的坐标为( , ),点D的坐标为( , );
(2)设点P的坐标为(a,0),当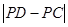 最大时,求a的值并在图中标出点P的位置;
最大时,求a的值并在图中标出点P的位置;
(3)在(2)的条件下,将△BCP沿x轴的正方向平移得到△B′C′P′,设点C对应点C′的横坐标为t(其中0<t<6),在运动过程中△B′C′P′与△BCD重叠部分的面积为S,求S与t之间的关系式,并直接写出当t为何值时S最大,最大值为多少?