如图,在四棱锥 中,侧棱
中,侧棱 底面
底面 ,底面
,底面 为矩形,
为矩形, 为
为 上一点,
上一点, ,
, .
.
(I)若 为
为 的中点,求证
的中点,求证 平面
平面 ;
;
(II)求三棱锥 的体积.
的体积.
(原创)已知等差数列 满足:
满足: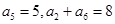 .
.
(1)求 的通项公式;
的通项公式;
(2)若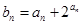 ,求数列
,求数列 的前
的前 项和
项和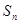 .
.
(原创)(本小题满分12分)已知数列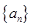 满足:
满足:
(1)求 的通项公式
的通项公式
(2)求证: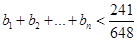
(原创)(本小题满分12分)已知点 点P在
点P在 轴上,点Q在
轴上,点Q在 轴正半轴上,点M在
轴正半轴上,点M在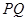 上,且满足
上,且满足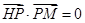 ,
, .
.
(1)当点P在 轴上移动时,求点M的轨迹方程C;
轴上移动时,求点M的轨迹方程C;
(2)给定圆N: 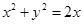 ,过圆心N作直线
,过圆心N作直线 ,此直线与圆N和(1)中的轨迹C共有四个交点,自上而下顺次记为A,B,C,D,如果线段
,此直线与圆N和(1)中的轨迹C共有四个交点,自上而下顺次记为A,B,C,D,如果线段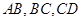 的长按此顺序构成一个等差数列,求直线
的长按此顺序构成一个等差数列,求直线 的方程。
的方程。
(本小题满分12分)已知函数 ,在区间
,在区间 内最大值为
内最大值为 ,
,
(1)求实数 的值;
的值;
(2)在 中,三内角A、B、C所对边分别为
中,三内角A、B、C所对边分别为 ,且
,且 ,求
,求 的取值范围.
的取值范围.
如图为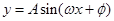 的图像的一段.(
的图像的一段.( )
)
(1)求其解析式;
(2)若将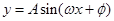 的图像向左平移
的图像向左平移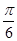 个单位长度后得
个单位长度后得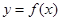 ,求
,求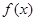 的对称轴方程.
的对称轴方程.