如图,已知椭圆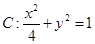 的上、下顶点分别为
的上、下顶点分别为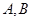 ,点
,点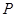 在椭圆上,且异于点
在椭圆上,且异于点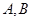 ,直线
,直线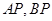 与直线
与直线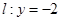 分别交于点
分别交于点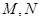 ,
,
(Ⅰ)设直线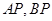 的斜率分别为
的斜率分别为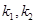 ,求证:
,求证: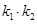 为定值;
为定值;
(Ⅱ)求线段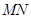 的长的最小值;
的长的最小值;
(Ⅲ)当点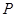 运动时,以
运动时,以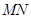 为直径的圆是否经过某定点?请证明你的结论.
为直径的圆是否经过某定点?请证明你的结论.
如图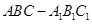 是一个斜三棱柱,已知
是一个斜三棱柱,已知 、平面
、平面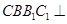 平面
平面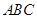 、
、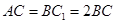 、
、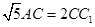 ,又
,又 、
、 分别是
分别是 、
、 的中点.
的中点.
(1)求证: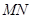 ∥平面
∥平面 ;
;
(2)求二面角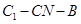 的大小.
的大小.
设P是⊙O: 上的一点,以
上的一点,以 轴的非负半轴为始边、OP为终边的角记为
轴的非负半轴为始边、OP为终边的角记为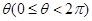 ,又向量
,又向量 .且
.且 .
.
(1)求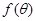 的单调减区间;网
的单调减区间;网
(2)若关于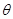 的方程
的方程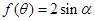 在
在 内有两个不同的解,求
内有两个不同的解,求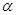 的取值范围.
的取值范围.
某公司招聘员工采取两次考试(笔试)的方法:第一试考选择题,共10道题(均为四选一题型),每题10分,共100分;第二试考解答题,共3题.规则是:只有在一试中达到或超过80分者才获通过并有资格参加二试,参加二试的人只有答对2题或3题才能被录用.现有甲、乙两人参加该公司的招聘考试.且已知在一试时:两人均会做10道题中的6道;对于另外4道题来说,甲有两题可排除两个错误答案、有两题完全要猜,乙有两题可排除一个错误答案、有一题可排除两个错误答案、有一题完全要猜.进入二试后,对于任意一题,甲答对的概率是 、乙答对的概率是
、乙答对的概率是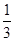 .
.
(1)分别求甲、乙两人能通过一试进入二试的概率 、
、 ;
;
(2)求甲、乙两人都能被录用的概率 .
.
已知函数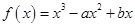 的图象与直线
的图象与直线 相切于点
相切于点 .
.
(1)求实数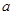 和
和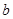 的值;
的值;
(2)求 的极值.
的极值.
已知函数 的反函数为
的反函数为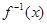 ,设
,设 的图象上在点
的图象上在点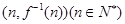 处的切线在y轴上的截距为
处的切线在y轴上的截距为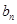 ,数列{
,数列{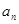 }满足:
}满足: .(1)求数列{
.(1)求数列{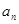 }的通项公式;
}的通项公式;
(2)在数列 中,仅
中,仅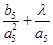 最小,求
最小,求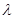 的取值范围;
的取值范围;
(3)令函数 数列
数列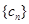 满足
满足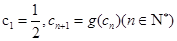 ,求证:对一切n≥2的正整数都有
,求证:对一切n≥2的正整数都有 .
.