如图(1),等腰直角三角形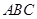 的底边
的底边 ,点
,点 在线段
在线段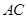 上,
上,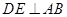 于
于 ,现将
,现将 沿
沿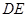 折起到
折起到 的位置(如图(2)).
的位置(如图(2)).
(Ⅰ)求证: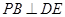 ;
;
(Ⅱ)若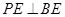 ,直线
,直线 与平面
与平面 所成的角为
所成的角为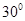 ,求
,求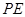 长.
长.
某种海洋生物身体的长度 (单位:米)与生长年限t(单位:年)
(单位:米)与生长年限t(单位:年)
满足如下的函数关系: .(设该生物出生时t=0)
.(设该生物出生时t=0)
(1)需经过多少时间,该生物的身长超过8米;
(2)设出生后第 年,该生物长得最快,求
年,该生物长得最快,求 的值.
的值.
已知函数 .
.
(1)若 ,求实数x的取值范围;
,求实数x的取值范围;
(2)求 的最大值.
的最大值.
在△ABC中,BC=a,AC=b,a、b是方程 的两个根,且
的两个根,且 ,求△ABC的面积及AB的长.
,求△ABC的面积及AB的长.
已知函数 过点
过点 .
.
(1)求实数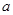 ;
;
(2)将函数 的图像向下平移1个单位,再向右平移
的图像向下平移1个单位,再向右平移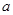 个单位后得到函数
个单位后得到函数 图像,设函数
图像,设函数 关于
关于 轴对称的函数为
轴对称的函数为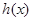 ,试求
,试求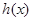 的解析式;
的解析式;
(3)对于定义在 上的函数
上的函数 ,若在其定义域内,不等式
,若在其定义域内,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知 .
.
(1)求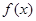 的最小值及取最小值时
的最小值及取最小值时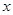 的集合;
的集合;
(2)求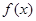 在
在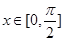 时的值域;
时的值域;
(3)求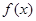 在
在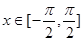 时的单调递减区间.
时的单调递减区间.