德阳中学数学竞赛培训共开设有初等代数、初等几何、初等数论和微积分初步共四门课程,要求初等代数、初等几何都要合格,且初等数论和微积分初步至少有一门合格,则能取得参加数学竞赛复赛的资格,现有甲、乙、丙三位同学报名参加数学竞赛培训,每一位同学对这四门课程考试是否合格相互独立,其合格的概率均相同,(见下表),且每一门课程是否合格相互独立,
| 课 程 |
初等代数 |
初等几何 |
初等数论 |
微积分初步 |
| 合格的概率 |
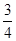 |
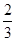 |
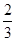 |
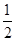 |
(1)求甲同学取得参加数学竞赛复赛的资格的概率;
(2)记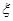 表示三位同学中取得参加数学竞赛复赛的资格的人数,求
表示三位同学中取得参加数学竞赛复赛的资格的人数,求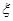 的分布列及期望
的分布列及期望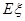 .
.
选修4—5:不等式选讲
已知正数a,b,c满足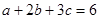 ,求证:
,求证: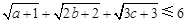 .
.
选修4-4:坐标系与参数方程(本小题满分10分)
在极坐标系中,已知曲线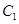 :
: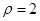 与曲线
与曲线 :
: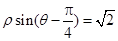 交于不同的两点
交于不同的两点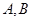 ,求
,求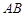 的值.
的值.
选修4—2:矩阵与变换 (本小题满分10分)
已知矩阵 ,
,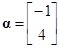 ,试计算:
,试计算: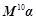 .
.
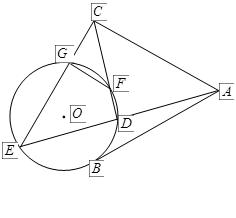
如图,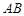 是⊙
是⊙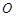 的一条切线,切点为
的一条切线,切点为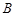 ,
,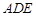 ,
,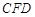 ,
,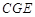 都是⊙
都是⊙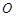 的割线,
的割线,
已知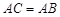 .
.
求证:
(1)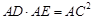 ;
;
(2)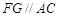 .
.
(本小题满分16分)
已知数列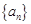 是各项均为正数的等差数列.
是各项均为正数的等差数列.
(1)若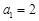 ,且
,且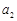 ,
,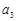 ,
,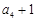 成等比数列,求数列
成等比数列,求数列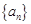 的通项公式
的通项公式 ;
;
(2)在(1)的条件下,数列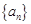 的前
的前 和为
和为 ,设
,设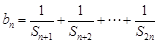 ,若对任意的
,若对任意的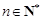 ,不等式
,不等式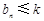 恒成立,求实数
恒成立,求实数 的最小值;
的最小值;
(3)若数列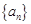 中有两项可以表示为某个整数
中有两项可以表示为某个整数 的不同次幂,求证:数列
的不同次幂,求证:数列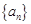 中存在无穷多项构成等比数列.
中存在无穷多项构成等比数列.