如图，将边长为4的等边三角形AOB放置于平面直角坐标系xoy中，F是AB边上的动点（不与端点A、B重合），过点F的反比例函数
（k＞0，x＞0）与OA边交于点E，过点F作FC⊥x轴于点C，连结EF、OF．
（1）若S△OCF=
，求反比例函数的解析式；
（2）在（1）的条件下，试判断以点E为圆心，EA长为半径的圆与y轴的位置关系，并说明理由；
（3）AB边上是否存在点F，使得EF⊥AE？若存在，请求出BF：FA的值；若不存在，请说明理由．
某工厂大楼后面紧邻着一个土坡，坡上面是一块平地，如图所示，BC∥AD，斜坡AB长20m，坡角∠BAD=60°，为了防止山体滑坡，保障安全，工厂决定对该土坡进行改造．经地质人员勘测，当坡角不超过45°时，可确保山体不滑坡．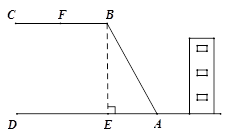
（1）求改造前坡顶与地面的距离BE的长；
（2）为确保安全，工厂计划改造时保持坡脚A不动，坡顶B沿BC削进到F点处，问BF至少是多少米？（结果均保留根号）
如图，□ABCD中，过点B作BG∥AC，在BG上取一点E，连结DE交AC的延长线于点F．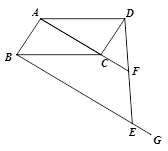
（1）求证：DF=EF；
（2）如果AD=2，∠ADC=60°，AC⊥DC于点C，AC=2CF，求BE的长．
学校为了解全校1600名学生到校上学的方式，在全校随机抽取了若干名学生进行问卷调查．问卷给出了五种上学方式供学生选择，每人只能选一项，且不能不选．将调查得到的结果绘制成如图所示的频数分布直方图和扇形统计图（均不完整）．
（1）在这次调查中，一共抽取了名学生；
（2）选择“步行”上学的学生有人；
（3）扇形统计图中，“私家车”所对应扇形的圆心角的度数为；
（4）估计全校所有学生中有多少人乘坐公交车上学．
化简代数式（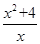
－4）÷ 
，当
满足
且为正整数时，求代数式的值.
（1）计算：
tan30°；（2）解方程：