如图，二次函数yax2bxc的图象的顶点C的坐标为(0,2)-优题课

题文

如图，二次函数 $y = a x^{2} + b x + c$ 的图象的顶点 $C$ 的坐标为 $(0, - 2)$ ，交 $x$ 轴于 $A$ 、 $B$ 两点，其中 $A (- 1, 0)$ ，直线 $l$ ： $x = m (m > 1)$ 与x轴交于 $D$ ．

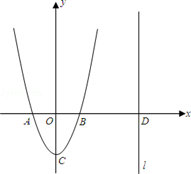
（1）求二次函数的解析式和 $B$ 的坐标；
（2）在直线 $l$ 上找点 $P$ （ $P$ 在第一象限），使得以 $P$ 、 $D$ 、 $B$ 为顶点的三角形与以 $B$ 、 $C$ 、 $O$ 为顶点的三角形相似，求点 $P$ 的坐标（用含 $m$ 的代数式表示）；
（3）在（2）成立的条件下，在抛物线上是否存在第一象限内的点 $Q$ ，使 $△ B P Q$ 是以 $P$ 为直角顶点的等腰直角三角形？如果存在，请求出点 $Q$ 的坐标；如果不存在，请说明理由．

科目数学题型解答题难度较难

知识点：二次函数在给定区间上的最值

登录免费查看答案和解析

相关试题

(每小题8分，共16分)
(1)先化简：，然后从，1，-1中选取一个能使结果为整数的数作为x的值代入求值．
(2)面对全球金融危机的挑战，我国政府毅然启动拉动内需的政策，改善民生．国务院决定从2009年2月1日起，“家电下乡”在全国范围内实施，农民购买入选产品，政府按原价购买总额的l3％给予补贴返还．某村委会组织部分农民到商场购买人选的同一型号的冰箱、电视机两种家电，已知购买冰箱的数量是电视机的2倍，且按原价购买冰箱总额为40000元、电视机总额为l5000元．根据“家电下乡”优惠政策，每台冰箱补贴返还的金额比每台电视机补贴返还的金额多65元，问：冰箱、电视机各购买多少台?

(每小题7分，共14分)
(1)计算：︱—2︱—(1+)⁰+；
x+3＞0
(2)解不等式组：
3(x-1)≤2x-1

(满分l4分)已知：抛物线y=x²-(a+2)x+9的顶点在坐标轴上．
(1)求a的值；
(2)若该抛物线的顶点C在x轴的正半轴上，而此抛物线与直线Y=x+9交于A，B两点，且A点在B点左侧，P为线段AB上的点(A，B两端点除外)．过点P作x轴的垂线与抛物线交于点Q(可在图中画示意图)．问：

①线段AB上是否存在这样的点P，使得PQ的长等于6?若存在，请求出点P的坐标；若不存在，请说明理由．
②线段AB上是否存在这样的点P，使得△ABQ∽△OAC?若存在，请求出此时点Q的坐标；若不存在，请说明理由．

(满分l2分)已知：如图，AB为⊙O的直径，AB=AC，BC交⊙O于点D，AC交⊙O于点E，∠BAC=45°．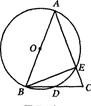

(1)求∠EBC的度数；
(2)求证：BD=CD．

(满分l2分)某中学对全校学生60s跳绳的次数进行了统计，全校学生的平均次数是l00次．某班体育委员统计了全班50名学生60s跳绳的成绩，列出的频数分布直方图如图所示(每个分组包括左端点，不包括右端点)．

(1)该班60s跳绳的平均次数是多少?是否超过全校的平均次数?
(2)该班一个学生说：“我的跳绳成绩在我班是中位数．”请你给出该生跳绳成绩所在的范围．
(3)从该班中任选一人，其跳绳次数达到或超过校平均次数的概率是多少?

试卷网试题网古诗词网作文网范文网