为积极响应市委,市政府提出的“实现伟大中国梦,建设美丽攀枝花”的号召,我市某校在八,九年级开展征文活动,校学生会对这两个年级各班内的投稿情况进行统计,并制成了如图所示的两幅不完整的统计图.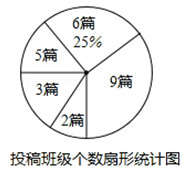
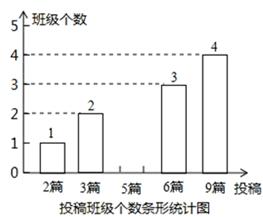
(1)求扇形统计图中投稿篇数为2所对应的扇形的圆心角的度数:
(2)求该校八,九年级各班在这一周内投稿的平均篇数,并将该条形统计图补充完整.
(3)在投稿篇数为9篇的两个班级中,八,九年级各有两个班,校学生会准备从这四个中选出两个班参加全市的表彰会,请你用列表法或画树状图的方法求出所选两个班正好不在同一年级的概率.
(1)计算:4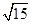 ×
×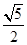 ÷
÷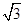 ﹣2sin30°﹣
﹣2sin30°﹣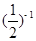
(2)化简: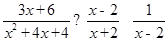 .
.
学校课外生物小组的试验园地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道(如图),要使种植面积为600平方米,求小道的宽.若设小道的宽为x米,则可列方程为 .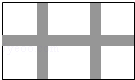
如图1,抛物线y=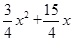 +3与x轴分别交于A、B两点(A在B的左侧),与y轴交于点C.
+3与x轴分别交于A、B两点(A在B的左侧),与y轴交于点C.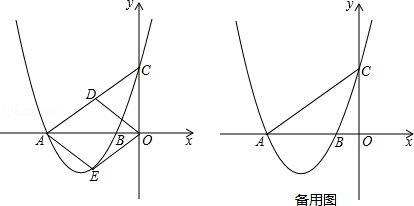
(1)求A、B、C三点的坐标;
(2)点D为线段AC上的一个动点(不与A、C两点重合),在运动的过程中,将△ADO以x轴为对称轴翻折,得到点D的对应点为E.
求:当点D的坐标为多少时,点E恰好落在抛物线的图象上?并判断此时的四边形AEOD是否为菱形?请说明理由.
(3)若点M(m,n)为抛物线上的动点,过点M作y轴的垂线,垂足为N,连接MC,则当m为何值时,△MCN和△AOC相似?请直接写出m的值(与△AOC重合的除外).
数学活动课上,老师给出如下问题:如图,将等腰直角三角形纸片沿斜边上的高AC剪开,得到等腰直角三角形△ABC与△EFD,将△EFD的直角顶点在直线BC上平移,在平移的过程中,直线AC与直线DE交于点Q,让同学们探究线段BQ与AD的数量关系和位置关系.
请你阅读下面交流信息,解决所提出的问题.
展示交流:
小敏:满足条件的图形如图甲所示图形,延长BQ与AD交于点H.我们可以证明△BCQ≌△ACD,从而易得BQ=AD,BQ⊥AD.
小慧:根据图甲,当点F在线段BC上时,我们可以验证小慧的说法是正确的.但当点F在线段CB的延长线上(如图乙)或线段CB的反向延长线上(如图丙)时,我对小慧说法的正确性表示怀疑.
(1)请你帮助小慧进行分析,小敏的结论在图乙、图丙中是否成立?请说明理由.
(选择图乙或图丙的一种情况说明即可).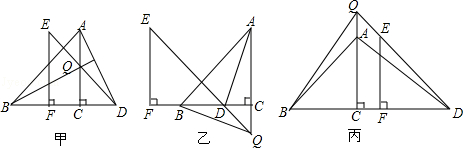
(2)小慧思考问题的方式中,蕴含的数学思想是 .
拓展延伸:
根据你上面选择的图形,分别取AB、BD、DQ、AQ的中点M、N、P、T.则四边形MNPT是什么样的特殊四边形?请说明理由.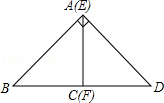
某体育用品公司以每件60元的批发价购回一批“电子智能跳绳”,第一周以每件120元的价格进行销售,第二周以每件110元的价格进行销售,结果两周共销售该款跳绳100件,两周共实现销售额11400元.
(1)求该公司第一周和第二周分别销售了电子智能跳绳多少件?
(2)为了追求利润的最大化,该公司决定第三周在第二周的基础上降价销售,公司营销部经过分析发现,如果第三周的销售价在第二周的基础上每降价1元,销售量则会在第二周的基础上增加2件,求第三周的销售价定为多少时,该周的销售利润最大?最大利润为多少元?