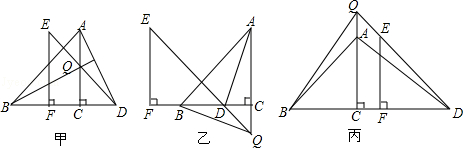
数学活动课上，老师给出如下问题：如图，将等腰直角三角形纸片沿斜边上的高AC剪开，得到等腰直角三角形△ABC与△EFD，将△EFD的直角顶点在直线BC上平移，在平移的过程中，直线AC与直线DE交于点Q，让同学们探究线段BQ与AD的数量关系和位置关系．
请你阅读下面交流信息，解决所提出的问题．
展示交流：
小敏：满足条件的图形如图甲所示图形，延长BQ与AD交于点H．我们可以证明△BCQ≌△ACD，从而易得BQ=AD，BQ⊥AD．
小慧：根据图甲，当点F在线段BC上时，我们可以验证小慧的说法是正确的．但当点F在线段CB的延长线上（如图乙）或线段CB的反向延长线上（如图丙）时，我对小慧说法的正确性表示怀疑．
（1）请你帮助小慧进行分析，小敏的结论在图乙、图丙中是否成立？请说明理由．
（选择图乙或图丙的一种情况说明即可）．

（2）小慧思考问题的方式中，蕴含的数学思想是            ．
拓展延伸：
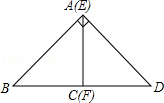
根据你上面选择的图形，分别取AB、BD、DQ、AQ的中点M、N、P、T．则四边形MNPT是什么样的特殊四边形？请说明理由．

科目 数学   题型 解答题   难度 较难

知识点： 圆内接四边形的性质