计算下列各式,然后回答问题:(x+3)(x+4)= ;(x+3)(x﹣4)= ;(x﹣3)(x+4)= ;(x﹣3)(x﹣4)= .
(1)根据以上的计算总结出规律:(x+m)(x+n)= ;
(2)运用(1)中的规律,直接写出下列结果:(x+25)(x﹣16)= .
如图, 中, ,点 , 在边 上, ,点 在 的延长线上, .
(1)求证: ;
(2)若 ,则 .

小李读一本名著,星期六读了36页,第二天读了剩余部分的 ,这两天共读了整本书的 ,这本名著共有多少页?
如图, 数轴上的点 , , , 表示的数分别为 , , 1 , 2 ,从 , , , 四点中任意取两点, 求所取两点之间的距离为 2 的概率 .

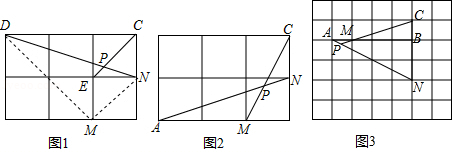
如图1,四边形 是矩形,点 的坐标为 ,点 的坐标为 ,点 从点 出发,沿 以每秒1个单位长度的速度向点 运动,同时点 从点 出发,沿 以每秒2个单位长度的速度向点 运动,当点 与点 重合时运动停止.设运动时间为 秒.
(1)当 时,线段 的中点坐标为 ;
(2)当 与 相似时,求 的值;
(3)当 时,抛物线 经过 , 两点,与 轴交于点 ,抛物线的顶点为 ,如图2所示,问该抛物线上是否存在点 ,使 ?若存在,求出所有满足条件的 的坐标;若不存在,说明理由.
问题呈现
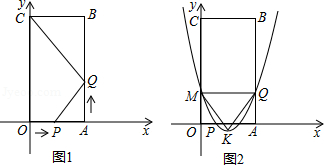
如图1,在边长为1的正方形网格中,连接格点 , 和 , , 和 相交于点 ,求 的值.
方法归纳
求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中 不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题,比如连接格点 , ,可得 ,则 ,连接 ,那么 就变换到 中.
问题解决
(1)直接写出图1中 的值为 2 ;
(2)如图2,在边长为1的正方形网格中, 与 相交于点 ,求 的值;
思维拓展
(3)如图3, , ,点 在 上,且 ,延长 到 ,使 ,连接 交 的延长线于点 ,用上述方法构造网格求 的度数.