两块完全相同的三角形纸板ABC和DEF,按如图所示的方式叠放,阴影部分为重叠部分,点O为边AC和DF的交点.不重叠的两部分△AOF与△DOC是否全等?为什么?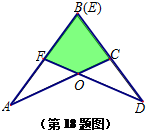
计算:
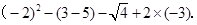
先化简,再求值:
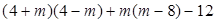 ,其中m=
,其中m=
在平面直角坐标系xOy中,抛物线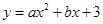 经过点N(2,-5),过点N作x轴的平行线交此抛物线左侧于点M,MN=6.
经过点N(2,-5),过点N作x轴的平行线交此抛物线左侧于点M,MN=6.求此抛物线的解析式
点P(x,y)为此抛物线上一动点,连接MP交此抛物线的对称轴于点D,当△DMN为直角三角形时,求点P的坐标;
设此抛物线与y轴交于点C,在此抛物线上是否存在点Q,使∠QMN=∠CNM ?若存在,求出点Q的坐标;若不存在,说明理由.
如图,四边形ABCD为矩形,AB=4,AD=3,动点M、N分别从D、B同时出发,以1个单位/秒的速度运动,点M沿DA向终点A运动,点N沿BC向终点C运动。过点N作NP⊥BC,交AC于点P,连结MP。已知动点运动了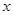 秒。
秒。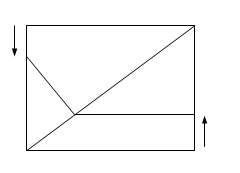
请直接写出PN的长;(用含
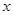 的代数式表示)
的代数式表示)若0秒≤
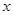 ≤3秒,试求△MPA的面积S与时间
≤3秒,试求△MPA的面积S与时间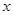 秒的函数关系式,并求S的最大值。
秒的函数关系式,并求S的最大值。若0秒≤
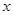 ≤3秒,△MPA能否与△PCN相似?若能,试求出相似时
≤3秒,△MPA能否与△PCN相似?若能,试求出相似时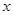 的对应值;若不能,试说明理由。
的对应值;若不能,试说明理由。
已知等腰△ABC中,AB=AC,D是BC的中点,将三角板中的90°角的顶点绕D点在△ABC内旋转,角的两边分别与AB、AC交于E、F,且点E、F不与A、B、C三点重合.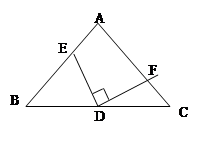
如果∠A=90°求证:DE=DF
如果DF//AB,则结论:“四边形AEDF为直角梯形”是否正确,若正确,请证明;若不正确,请画出草图举反例