如图,四边形ABCD为矩形,AB=4,AD=3,动点M、N分别从D、B同时出发,以1个单位/秒的速度运动,点M沿DA向终点A运动,点N沿BC向终点C运动。过点N作NP⊥BC,交AC于点P,连结MP。已知动点运动了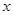 秒。
秒。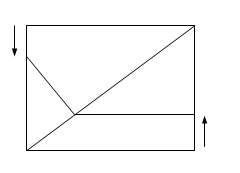
请直接写出PN的长 ;(用含
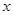 的代数式表示)
的代数式表示)若0秒≤
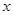 ≤3秒,试求△MPA的面积S与时间
≤3秒,试求△MPA的面积S与时间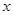 秒的函数关系式,并求S的最大值。
秒的函数关系式,并求S的最大值。若0秒≤
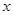 ≤3秒,△MPA能否与△PCN相似?若能,试求出相似时
≤3秒,△MPA能否与△PCN相似?若能,试求出相似时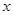 的对应值;若不能,试说明理由。
的对应值;若不能,试说明理由。
如图,一架飞机由 向 沿水平直线方向飞行,在航线 的正下方有两个山头 .飞机在 处时,测得山头 恰好在飞机的正下方,山头 在飞机前方,俯角为 .飞机飞行了 到 处时,往后测得山头 的俯角分别为 和 .已知山头 的海拔高度为 ,求山头 的海拔高度.(精确到 ,已知 )

南海诸岛自古以来都是中国的领土,4月12日,中央军委在南海海域隆重举行海上阅兵,军委主席登上长沙舰检阅海军舰艇编队,包括辽宁号航母在内的48艘舰艇参加了阅兵仪式.如图, 是两处海港,其中 在 东偏南 方向 处,辽宁号航母从海港 出发,沿东偏北 方向,以 的速度匀速航行,两小时后,长沙舰从海港 出发,沿东偏北 的方向匀速航行,两舰恰好同时到达阅兵地点 .
(1)长沙舰从海港出发航行到达阅兵地点用了多长时间?
(2)求长沙舰的航行速度(结果保留根号).

如图, 是以 为直径的 上一点,过点 的切线 交 的延长线于点 ,过点 作 交 的延长线于点 ,垂足为点 .
(1)求证: ;
(2)若 的直径 为 .
①求线段 的长;
②求线段 的长.

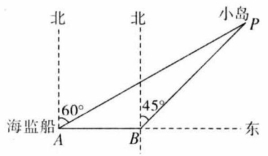
某海域有一小岛 ,在以 为圆心,半径 为 海里的圆形海域内有暗礁.一海监船自西向东航行,它在 处测得小岛 位于北偏东 的方向上,当海监船行驶 海里后到达 处,此时观测小岛 位于 处北偏东 方向上.
(1)求 之间的距离 ;
(2)若海监船由 处继续向东航行是否有触礁危险?请说明理由.如果有触礁危险,那么海监船由 处开始沿南偏东至多少度的方向航行能安全通过这一海域?
如图,矩形 的对角线 相交于点 ,过点 作 交 于点 ,若 的面积为 ,求 的值.
