如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C
(1)求抛物线的函数解析式.
(2)设点D在抛物线上,点E在抛物线的对称轴上,且以AO为边的四边形AODE是平行四边形,求点D的坐标.
(3)P是抛物线上第一象限内的动点,过点P作PM⊥x轴,垂足为M,是否存在点P,使得以P,M,A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
(本小题满分10分)李华在学校组织的社会调查活动中负责了解他所居住的小区600户居民的家庭收入情况.他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
| 分组 |
频数 |
百分比 |
 |
2 |
5% |
800 1000 1000 |
6 |
15% |
1000 12000 12000 |
45% |
|
| 9 |
22.5% |
|
1600 1800 1800 |
2 |
|
| 合计 |
40 |
100% |

根据以上提供的信息,解答下列问题:
(1)补全频数分布表.
(2)补全频数分布直方图.
(3)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
(本小题满分8分)如图,EF∥AD,∠1=∠2,∠BAC=70°。求∠AGD.请将解题过程填写完整。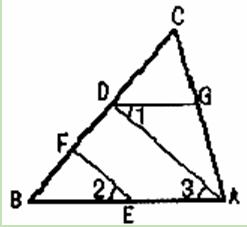
因为EF∥AD,(已知)
所以∠2=_________.()
又因为∠1=∠2,(已知)
所以∠1=∠3.()
所以AB//________.()
所以∠BAC+_______=180°.()
又因为∠BAC=70°,(已知)
所以∠AGD=________.
(本题每小题5分,满分10分)
(1)解方程组:
(2)解不等式组
(本小题满分12分)为了防控甲型H1N1流感,某校积极进行校园环境消毒,购买了甲乙两种消毒液共100瓶,其中甲种消毒液6元/瓶,乙种消毒液9元/瓶。
(1)如果购买这两种消毒液共用780元,求四甲乙两种消毒液各购买了多少瓶?
(2)该校准备在购买这两种消毒液(不包括已购买的100瓶)使已种瓶数是甲种瓶数的2倍,且所需费用不超过1200元(不包括780元)求甲种消毒液最多能再购买多少瓶?
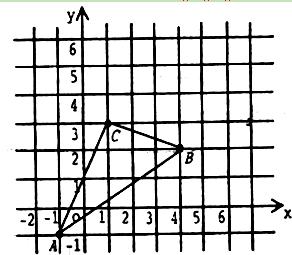
(本小题满分10分)如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)求出△ABC的面积S△ABC.
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A’B’C’,在图中画出△ABC变化位置,并写出△A’B’C’的坐标