如图,已知直线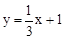 与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.
与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.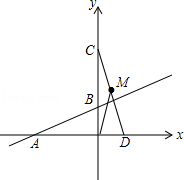
(1)点C的坐标是 ,线段AD的长等于 ;
(2)点M在CD上,且CM=OM,抛物线y=x2+bx+c经过点G,M,求抛物线的解析式;
(3)如果点E在y轴上,且位于点C的下方,点F在直线AC上,那么在(2)中的抛物线上是否存在点P,使得以C,E,F,P为顶点的四边形是菱形?若存在,请求出该菱形的周长l;若不存在,请说明理由.
(1)如图1,OC平分∠AOB,点P在OC上,若⊙P与OA相切,那么⊙P与OB位置关系是.
(2)如图2,⊙O的半径为2,∠AOB=120°,
①若点P是⊙O上的一个动点,当PA=PB时,是否存在⊙Q,同时与射线PA.PB相切且与⊙O相切,如果存在,求出⊙Q的半径; 如果不存在,请说明理由.
②若点P在BO的延长线上,且满足PA⊥PB,是否存在⊙Q,同时与射线PA.PB相切且与⊙O相切,如果存在,请直接写出⊙Q的半径; 如果不存在,请说明理由.
阅读下列材料:
小华遇到这样一个问题,如图1,△ABC中,∠ACB=30º,BC=6,AC=5,在△ABC内部有一点P,连接PA.PB.PC,求PA+PB+PC的最小值.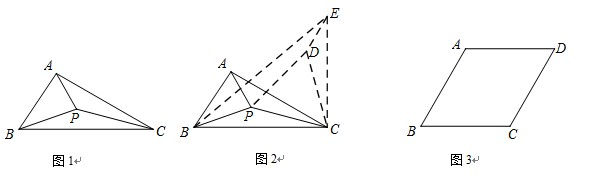
小华是这样思考的:要解决这个问题,首先应想办法将这三条端点重合于一点的线段分离,然后再将它们连接成一条折线,并让折线的两个端点为定点,这样依据“两点之间,线段最短”,就可以求出这三条线段和的最小值了.他先后尝试了翻折.旋转.平移的方法,发现通过旋转可以解决这个问题.他的做法是,如图2,将△APC绕点C顺时针旋转60º,得到△EDC,连接PD.BE,则BE的长即为所求.
(1)请你写出图2中,PA+PB+PC的最小值为 ;
(2)参考小华的思考问题的方法,解决下列问题:
①如图3,菱形ABCD中,∠ABC=60º,在菱形ABCD内部有一点P,请在图3中画出并指明长度等于PA+PB+PC最小值的线段(保留画图痕迹,画出一条即可);
②若①中菱形ABCD的边长为4,请直接写出当PA+PB+PC值最小时PB的长.
如图,在矩形ABCD中,点O是边AD上的中点,点E是边BC上的一个动点,延长EO到F,使得OE=OF.
(1)当点E运动到什么位置时,四边形AEDF是菱形?(直接写出答案)
(2)若矩形ABCD的周长为20,四边形AEDF的面积是否存在最大值?如果存在,请求出最大值;如果不存在,请说明理由.
(3)若AB=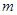 ,BC=
,BC=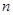 ,当
,当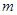 .
.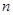 满足什么条件时,四边形AEDF能成为一个矩形?(不必说明理由)
满足什么条件时,四边形AEDF能成为一个矩形?(不必说明理由)
某批发商以每件50元的价格购进400件T恤.若以单价70元销售,预计可售出200件.批发商的销售策略是:第一个月为增加销售量,降价销售,经过市场调查,单价每降低0.5元,可多售出5件,但最低单价不低于购进的价格;第一个月结束后,将剩余的T恤一次性清仓销售,清仓时单价为40元.设第一个月单价降低x元.
(1)根据题意,完成下表:
| 每件T恤的利润(元) |
销售量(件) |
|
| 第一个月 |
||
| 清仓时 |
(2)T恤的销售单价定为多少元时,该批发商可获得最大利润?最大利润为多少?
如图,已知△ABC内接于⊙O,点D在OC的延长线上,∠B=∠CAD=30°.
(1)AD是⊙O的切线吗?为什么?
(2)若OD⊥AB,BC=5,求⊙O的半径.