(1)如图1,OC平分∠AOB,点P在OC上,若⊙P与OA相切,那么⊙P与OB位置关系是 .
(2)如图2,⊙O的半径为2,∠AOB=120°,
①若点P是⊙O上的一个动点,当PA=PB时,是否存在⊙Q,同时与射线PA.PB相切且与⊙O相切,如果存在,求出⊙Q的半径; 如果不存在,请说明理由.
②若点P在BO的延长线上,且满足PA⊥PB,是否存在⊙Q,同时与射线PA.PB相切且与⊙O相切,如果存在,请直接写出⊙Q的半径; 如果不存在,请说明理由.
(本题6分),(湖南湘西,19,6分)如图,已知AC平分 BAD,AB=AD。求证:△ABC≌△ADC
BAD,AB=AD。求证:△ABC≌△ADC
(本题5分)(湖南湘西,18,5分)解不等式组: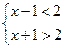 并把它的解集在数轴上表示出来。
并把它的解集在数轴上表示出来。
如图,抛物线y=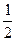 x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0). 27
27
⑴求抛物线的解析式及顶点D的坐标;
⑵判断△ABC的形状,证明你的结论;
⑶点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.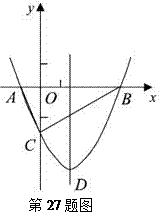
已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
⑴求证:点D是AB的中点;
⑵判断DE与⊙O的位置关系,并证明你的结论;
⑶若⊙O的直径为18,cosB = ,求DE的长.
,求DE的长.
某班到毕业时共结余班费1800元,班委会决定拿出不少于270元但不超过300元的资金为老师购买纪念品,其余资金用于在毕业晚会上给50位同学每人购买一件T恤或一本影集作为纪念品.已知每件T恤比每本影集贵9元,用200元恰好可以买到2件T恤和5本影集.
⑴求每件T恤和每本影集的价格分别为多少元?
⑵有几种购买T恤和影集的方案?