在平面直角坐标系中,已知M1(3,2),N1(5,﹣1),线段M1N1平移至线段MN处(注:M1与M,N1与N分别为对应点).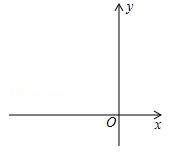
(1)若M(﹣2,5),请直接写出N点坐标.
(2)在(1)问的条件下,点N在抛物线 上,求该抛物线对应的函数解析式.
上,求该抛物线对应的函数解析式.
(3)在(2)问条件下,若抛物线顶点为B,与y轴交于点A,点E为线段AB中点,点C(0,m)是y轴负半轴上一动点,线段EC与线段BO相交于F,且OC:OF=2: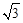 ,求m的值.
,求m的值.
(4)在(3)问条件下,动点P从B点出发,沿x轴正方向匀速运动,点P运动到什么位置时(即BP长为多少),将△ABP沿边PE折叠,△APE与△PBE重叠部分的面积恰好为此时的△ABP面积的 ,求此时BP的长度.
,求此时BP的长度.
已知 是关于x的一元二次方程
是关于x的一元二次方程 的两个实数根,且
的两个实数根,且 ,
,
求:(1)k的值;
(2) 的值.
的值.
如图,△ABC三个顶点的坐标分别为A(-3,-1)、B(-4,-3)C(-2,-5):
(1)在图中作出△ABC关于y轴对称的图形△A1B1C1;并写出A1、B1、C1点的坐标。
(2)在图中作出△ABC关于原点对称的图形△A2B2C2;并写出A2、B2、C2点的坐标.
先化简,再求值:(x-1)÷ ,其中x为方程x2+3x+2=0的根.
,其中x为方程x2+3x+2=0的根.
如图,在菱形ABCD中,AC、BD交于点O,AC=12cm,BD=16cm。动点P在线段AB上,由B向A运动,速度为1cm/s,动点Q在线段OD上,由D向O运动,速度为1cm/s。过点Q作直线EF┴BD交AD于E,交CD于F,连接PF,设运动时间为t(0<t<8)。问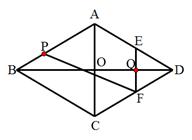
(1)何时四边形APFD为平行四边形?求出相应t的值;
(2)设四边形APFE面积为ycm2,求y与t的函数关系式;.
(3)是否存在某一时刻t,使S四边形APFE:S菱形ABCD=17:40?若存在,求出相应t的值,并求出,P、E两点间的距离,若不存在,说明理由。
将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].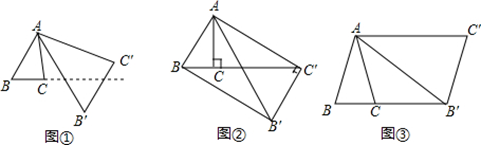
(1)如图①,对△ABC作变换[60°,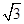 ]得△AB′C′,则S△AB′C′:S△ABC=;直线BC与直线B′C′所夹的锐角为度;
]得△AB′C′,则S△AB′C′:S△ABC=;直线BC与直线B′C′所夹的锐角为度;
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,BC=1,对△ABC 作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.