已知:直线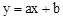 过抛物线
过抛物线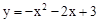 的顶点P,如图所示.
的顶点P,如图所示.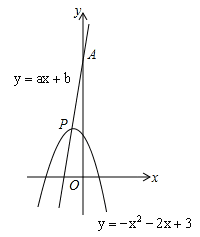
(1)顶点P的坐标是 ;
(2)若直线y=ax+b经过另一点A(0,11),求出该直线的表达式;
(3)在(2)的条件下,若有一条直线y=mx+n与直线y=ax+b关于x轴成轴对称,求直线y=mx+n与抛物线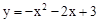 的交点坐标.
的交点坐标.
计算: .
如图,在 中, ,以 的边 为直径作 ,交 于点 ,过点 作 ,垂足为点 .
(1)试证明 是 的切线;
(2)若 的半径为5, ,求此时 的长.

如图,已知反比例函数 的图象与直线 相交于点 , .
(1)求出直线 的表达式;
(2)在 轴上有一点 使得 的面积为18,求出点 的坐标.

如图,小莹在数学综合实践活动中,利用所学的数学知识对某小区居民楼 的高度进行测量,先测得居民楼 与 之间的距离 为 ,后站在 点处测得居民楼 的顶端 的仰角为 ,居民楼 的顶端 的仰角为 ,已知居民楼 的高度为 ,小莹的观测点 距地面 .求居民楼 的高度(精确到 .(参考数据: , , .

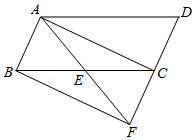
如图,在 中, 为 的中点,连接 并延长交 的延长线于点 ,连接 , ,若 ,求证:四边形 是矩形.