如图，在平面直角坐标系中有一矩形ABCO（O为原点），点A、C分别在x轴、y轴上，且C点坐标为(0，6)，将△BCD沿BD折叠(D点在OC边上），使C点落在DA边的E点上，并将△BAE沿BE折叠，恰好使点A落在BD边的F点上．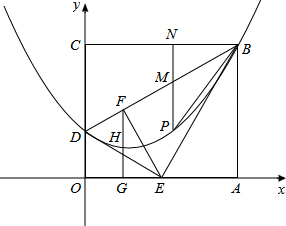
（1）求BC的长，并求折痕BD所在直线的函数解析式；
（2）过点F作FG⊥x轴，垂足为G，FG的中点为H，若抛物线
经过B,H, D三点，求抛物线解析式；
（3）点P是矩形内部的点，且点P在（2）中的抛物线上运动（不含B, D点），过点P作PN⊥BC，分别交BC 和 BD于点N, M，是否存在这样的点P，使
如果存在，求出点P的坐标；如果不存在，请说明理由．
如图，已知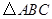
的三个顶点的坐标分别为
、
、
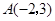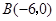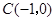．请直接写出点
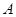关于原点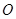
对称的点的坐标；将
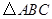绕坐标原点逆时针旋转90°．画出图形，直接写出点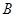
的对应点的坐标；请直接写出：以
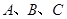为顶点的平行四边形的第四个顶点
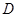的坐标．
黄冈市某楼盘准备以每平方米6000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米4860元的均价开盘销售。求平均每次下调的百分率。
某人准备以开盘价均价购买一套100平方米的住房，开发商给予以下两种优惠方案以供选择：①打9.8折销售；②不打折，一次性送装修费每平方米80元，试问哪种方案更优惠？
已知抛物线
与x轴的一个交点为A(-1，0)，与y轴正半轴交于点C．
直接写出抛物线的对称轴，及抛物线与
轴的另一个交点B的坐标；当∠ACB=90°时，求抛物线的解析式；
抛物线上是否存在点M，使得△ABM和△ABC的面积相等（△ABM与△ABC重合除外）？若存在，请直接写出点M坐标；若不存在，请说明理由．
在第一象限内，抛物线上是否存在点N，使得△BCN的面积最大？若存在，求出这个最大值和点N坐标；若不存在，请说明理由．
如图1，Rt△ABC中，∠ACB=90°，AC=3，BC=4，点O是斜边AB上一动点，以OA为半径作⊙O与AC边交于点P，
当OA=
时，求点O到BC的距离如图2，当OA=
时，求证：直线BC与⊙O相切；此时线段AP的长是多少？
若BC边与⊙O有公共点，直接写出 OA
的取值范围；若CO平分∠ACB，则线段AP的长是多少？
如图1，正方形ABCD的边长为1，点E是AD边的中点，将△ABE沿BE翻折得到△FBE，延长BF交CD边于点G，则FG=DG，求出此时DG的值；
如图2，矩形ABCD中，AD>AB，AB=1，点E是AD边的中点，同样将△ABE沿BE翻折得到△FBE，延长BF交CD边于点G．
①证明：FG=DG；
②若点G恰是CD边的中点，求AD的值；
③若△ABE与△BCG相似，求AD的值．