如图，在直角体系中，直线AB交x轴于点A（5，0），交y轴于点B，AO是⊙M的直径，其半圆交AB于点C，且AC=3。取BO的中点D，连接CD、MD和OC。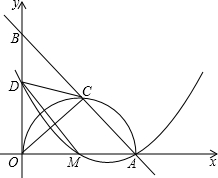
（1）求证：CD是⊙M的切线；
（2）二次函数的图象经过点D、M、A，其对称轴上有一动点P，连接PD、PM，求△PDM的周长最小时点P的坐标；
（3）在（2）的条件下，当△PDM的周长最小时，抛物线上是否存在点Q，使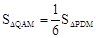
？若存在，求出点Q的坐标；若不存在，请说明理由。
小明家今年种植的“红灯”樱桃喜获丰收，采摘上市20天全部销售完，小明对销售情况进行跟踪记录，并将记录情况绘成图象，日销售量y（单位：千克）与上市时间x（单位：天）的函数关系如图1所示，樱桃价格z（单位：元/千克）与上市时间x（单位：天）的函数关系式如图2所示．
（1）观察图象，直接写出日销售量的最大值；
（2）求小明家樱桃的日销售量y与上市时间x的函数解析式；
（3）试比较第10天与第12天的销售金额哪天多？
如图，点A．B．C分别是⊙O上的点，∠B=60°，AC=3，CD是⊙O的直径，P是CD延长线上的一点，且AP=AC．
（1）求证：AP是⊙O的切线；
（2）求PD的长．
如图，点A．F、C．D在同一直线上，点B和点E分别在直线AD的两侧，且
AB=DE，∠A=∠D，AF=DC．
（1）求证：四边形BCEF是平行四边形，
（2）若∠ABC=90°，AB=4，BC=3，当AF为何值时，四边形BCEF是菱形．
某工厂加工某种产品．机器每小时加工产品的数量比手工每小时加工产品的数量的2倍多9件，若加工1800件这样的产品，机器加工所用的时间是手工加工所用时间的
倍，求手工每小时加工产品的数量．
“最美女教师”张丽莉，为抢救两名学生，以致双腿高位截肢，社会各界纷纷为她捐款，我市某中学九年级一班全体同学参加了捐款活动，该班同学捐款情况的部分统计图如图所示：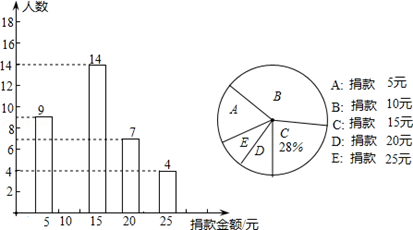
（1）求该班的总人数；
（2）将条形图补充完整，并写出捐款总额的众数；
（3）该班平均每人捐款多少元？