某镇水库的可用水量为12000万m3,假设年降水量不变,能维持该镇16万人20年的用水量.为实施城镇化建设,新迁入了4万人后,水库只能够维持居民15年的用水量.
(1)问:年降水量为多少万m3?每人年平均用水量多少m3?
(2)政府号召节约用水,希望将水库的使用年限提高到25年.则该镇居民人均每年需节约多少m3水才能实现目标?
(3)某企业投入1000万元设备,每天能淡化5000m3海水,淡化率为70%.每淡化1m3海水所需的费用为1.5元,政府补贴0.3元.企业将淡化水以3.2元/m3的价格出售,每年还需各项支出40万元.按每年实际生产300天计算,该企业至少几年后能收回成本(结果精确到个位)?
完成下列解答过程:
证明:(1)∵∠A=_______,(已知)
∴AC∥ED.(_______)
(2)∵∠EDF=_______,(已知)
∴AC∥ED.(_______)
(3)∵∠A+∠DFA=180°(已知)
∴_______∥_______.(_______)
如图,已知a∥b,∠3+∠2=180°,b与c平行吗?说明理由.
先作图,再证明.
(1)在所给的图形(如图)中完成下列作图(保留作图痕迹)
①作∠ACB的平分线CD,交AB于点D;
②延长BC到点E,使CE=CA,连接AE;
(2)求证:CD∥AE.
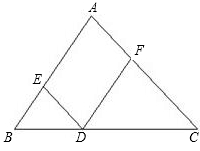
如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,将△ADC沿AC边所在的直线折叠,使点D落在点E处,得四边形ABCE.
求证:EC∥AB.
如图所示,在一个凹型图形中,下列说法都正确吗?如果不正确,请加以更正.
(1)∠H与∠A是同旁内角,∠H与∠G是内错角;
(2)与∠D互为同旁内角的角只有∠C;
(3)图中没有同位角.