已知椭圆 的长轴两端点分别为
的长轴两端点分别为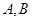 ,
, 是椭圆上的动点,以
是椭圆上的动点,以 为一边在
为一边在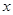 轴下方作矩形
轴下方作矩形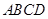 ,使
,使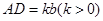 ,
,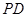 交
交 于点
于点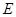 ,
,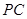 交
交 于点
于点 .
.
(Ⅰ)如图(1),若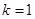 ,且
,且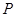 为椭圆上顶点时,
为椭圆上顶点时, 的面积为12,点
的面积为12,点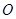 到直线
到直线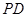 的距离为
的距离为 ,求椭圆的方程;
,求椭圆的方程;
(Ⅱ)如图(2),若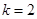 ,试证明:
,试证明: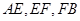 成等比数列.
成等比数列.
(本小题满分12分)
已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点。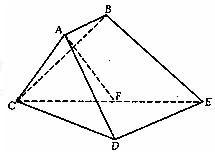
(1)求证:AF⊥CD;
(2)求直线AC与平面CBE所成角的大小。
(本小题满分12分)
已知函数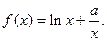
(1)当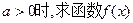 的单调区间;
的单调区间;
(2)若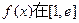 上的最小值为1,求实数a的取值范围;(其中e为自然对数的底数)
上的最小值为1,求实数a的取值范围;(其中e为自然对数的底数)
(3)若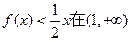 上恒成立,求实数a的取值范围。
上恒成立,求实数a的取值范围。
(本小题满分12分)
2009年我市城市建设取得最大进展的一年,正式拉开了从“两湖”时代走向“八里湖”时代的大幕。为了建设大九江的城市框架,市政府大力发展“八里湖”新区,现有甲乙两个项目工程待建,请三位专家独立评审。假设每位专家评审结果为“支持”或“不支持”的概率都是 ,每个项目每获得一位专家“支持”则加1分,“不支持”记为0分,令
,每个项目每获得一位专家“支持”则加1分,“不支持”记为0分,令 表示两个项目的得分总数。
表示两个项目的得分总数。 (1)求甲项目得1分乙项目得2分的概率;
(1)求甲项目得1分乙项目得2分的概率;
(2)求 的数学期望E
的数学期望E 。
。
(本小题满 分12分)
分12分)
已知函数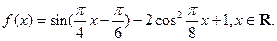
(1)求函 数
数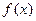 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(2)若关于x的方程 内有实数解,求实数m的取值范围。
内有实数解,求实数m的取值范围。
(本小题满分14分)
设数列 ,
, 满足:a1=4,a2=
满足:a1=4,a2= ,
, ,
,  .
.
(1)用 表示
表示 ;并证明:
;并证明: , an>2 ;
, an>2 ;
(2)证明: 是等比数列;
是等比数列;
(3)设Sn是数列 的前n项和,当n≥2时,Sn与
的前n项和,当n≥2时,Sn与 是否有确定的大小关系?若有,加以证明;若没有,请说明理由.
是否有确定的大小关系?若有,加以证明;若没有,请说明理由.