如图(甲)所示的轮轴,它可以绕垂直于纸面的光滑固定水平轴O转动。轮上绕有轻质柔软细线,线的一端系一重物,另一端系一质量为m的金属杆。在竖直平面内有间距为L的足够长的平行金属导轨PQ、EF,在QF之间连接有阻值为R的电 阻,其余电阻不计,磁感应强度为B的匀强磁场与导轨平面垂直。开始时金属杆置于导轨下端,将质量为M的重物由静止释放,重物最终能匀速下降。运动过程中金属杆始终与导轨垂直且接触良好,忽略所有摩擦。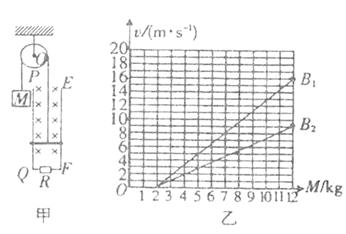
(1)重物匀速下降的速度V的大小是多少?
(2)对一定的磁感应强度B,重物的质量M取不同的值,测出相应的重物做匀速运动时的速度,可得出v-M实验图线。图(乙)中画出了磁感应强度分别为B1和B2时的两条实验图线,试根据实验结果计算B1和B2的比值。
(3)若M从静止到匀速的过程中一目下降的高度为h,求这一过程中R上产生的焦耳热
吴菊萍徒手勇救小妞妞,被誉为“最美妈妈”.设妞妞的质量m=10kg,从离地h= 28.5m高的阳台掉下,下落过程中空气阻力约为本身重力的0.4倍;在妞妞开始掉下时,吴菊萍立刻从静止开始匀加速奔跑水平距离s =9m到达楼下,恰好张开双臂在距地面高度为h2=1.5m处接住妞妞,缓冲到地面时速度为零,缓冲过程中的空气阻力不计。g取10m/s2,求:
妞妞在被接到前下落的时间.
吴菊萍跑到楼下时的速度.
在缓冲过程中吴菊萍对妞妞做的功.
如图所示,用两根轻绳和一根轻弹簧将质量均为m的A、B两小球以及水平天花板上的固定点O之间两两连接,然后用一水平方向的恒力作用于A球上,此时两根轻绳均处于直线状态,且OB绳恰好处于竖直方向,两球均处于静止状态。已知三段长度之比为OA:AB:OB =3:4:5,重力加速度为g 。试确定:
弹簧OA的拉力.
若突然将恒力撤去,则撤去瞬间,小球A的加速度.
某同学想要了解导线在质量相同时,电阻与截面积的关系,选取了材料相同、质量相等的5卷导线,进行了如下实验: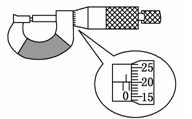
用螺旋测微器测量某一导线的直径如图所示.读得直径d=__________ mm.
该同学经实验测量及相关计算得到如下数据:
| 电阻R(Ω) |
121.0 |
50.0 |
23.9 |
10.0 |
3.1 |
| 导线直径d(mm) |
0.801 |
0.999 |
1.201 |
1.494 |
1.998 |
| 导线截面积S(mm2) |
0.504 |
0.784 |
1.133 |
1.753 |
3.135 |
请你根据以上数据判断,该种导线的电阻R与截面积S应满足的关系.若导线的电阻率ρ=5.1×10-7 Ω·m,则表中阻值为3.1 Ω的导线长度l=________
m(结果保留两位有效数字).
如图所示,第四象限内有互相正交的匀强电场E与匀强磁场B1, E的大小为0.5×103V/m, B1大小为0.5T;第一象限的某个矩形区域内,有方向垂直纸面向里的匀强磁场B2,磁场的下边界与x轴重合.一质量m=1×10-14kg、电荷量q=1×10-10C的带正电微粒以某一速度v沿与y轴正方向60°角从M点沿直线运动,经P点即进入处于第一象限内的磁场B2区域.一段时间后,小球经过y轴上的N点并与y轴正方向成60°角的方向飞出。M点的坐标为(0,-10),N点的坐标为(0,30),不计粒子重力,g取10m/s2.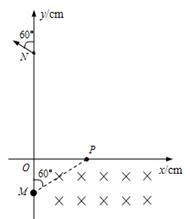
请分析判断匀强电场E的方向(要求在图中画出)并求出微粒的运动速度v;
匀强磁场B2的大小为多大?
B2磁场区域的最小面积为多少?
如图所示,光滑绝缘水平面AB与倾角θ=370,长L=6m的绝缘斜面BC在B处圆滑相连,在斜面的C处有一与斜面垂直的弹性绝缘挡板,质量m=0.5kg、所带电荷量q=5x10-5C的绝缘带电滑块置于斜面的中点D, 整个空间存在水平向右的匀强电场,场强E=2×l05N/C,现让滑块以v0=12m/s的速度沿斜面向上运动。设滑块与挡板碰撞前后所带电荷量不变、速度大小不变,滑块和斜面间的动摩擦因数 ,求:
,求: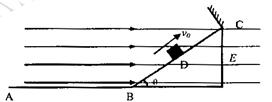
滑块第一次与挡板碰撞时的速度大小;
滑块第一次与挡板碰撞后能达到左端的最远点离B点的距离;
滑块运动的总路程。