已知椭圆C长轴的两个顶点为A(-2,0),B(2,0),且其离心率为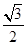 .
.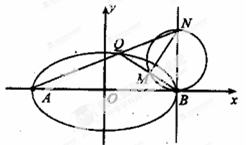
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若N是直线x=2上不同于点B的任意一点,直线AN与椭圆C交于点Q,设直线QB与以NB为直径的圆的一个交点为M(异于点B),求证:直线NM经过定点.
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.已知函数f(x)=ax2+(b+1)x+b﹣1(a≠0).
(1)当a=1,b=﹣2时,求f(x)的不动点;
(2)若对于任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围.
已知定义域为R的奇函数f(x),当x>0时,f(x)=x2﹣3.
(1)当x<0时,求函数f(x)的解析式;
(2)求函数f(x)在R上的解析式;
(3)解方程f(x)=2x.
根据条件求下列各函数的解析式:
(1)已知f(x)是二次函数,若f(0)=0,f(x+1)=f(x)+x+1,求f(x).
(2)已知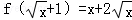 ,求f(x)
,求f(x)
(3)若f(x)满足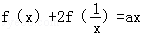 ,求f(x).
,求f(x).
已知集合A={x|x2﹣2x﹣3≤0,x∈R},B={x|x2﹣2mx+m2﹣4≤0,x∈R,m∈R}.
(1)若A∩B=[0,3],求实数m的值;
(2)若A⊆∁RB,求实数m的取值范围.
把一颗骰子投掷2次,观察出现的点数,并记第一次出现的点数为a,第二次出现的点数为b,试就方程组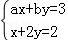 解答下列各题:
解答下列各题:
(1)求方程组只有一个解的概率;
(2)求方程组只有正数解的概率.