已知数列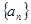 的前
的前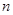 项和为
项和为 ,数列
,数列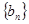 的首项
的首项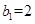 ,且点
,且点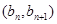 在直线
在直线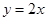 上.
上.
(1)求数列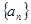 ,
,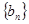 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列 的前
的前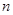 项和
项和 .
.
盒子装中有形状、大小完全相同的五张卡片,分别标有数字1,2,3,4,5.现每次从中任意抽取一张,取出后不再放回.
(1)若抽取三次,求前两张卡片所标数字之和为偶数的条件下,第三张为奇数的概率;
(2)若不断抽取,直至取出标有偶数的卡片为止,设抽取次数为ξ,求随机变量ξ的分布列及数学期望.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠ABC=60º,又PA⊥底面ABCD,AB=2PA,E为BC的中点.
(1)求证:AD⊥PE;
(2)求平面APE与平面PCD所成锐二面角的余弦值.
在四边形ABCD中,AD⊥CD,AD=5,AB=7,∠BDA=60º,∠CBD=15º,求BC长.
已知函数f(x)=|x+a|+|x﹣2|
(1)当a=﹣3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x﹣4|的解集包含[1,2],求a的取值范围.
在直角坐标系xOy中,直线l的参数方程为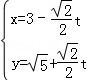 (t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为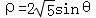 .
.
(Ⅰ)求圆C的圆心到直线l的距离;
(Ⅱ)设圆C与直线l交于点A、B.若点P的坐标为(3,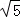 ),求|PA|+|PB|.
),求|PA|+|PB|.