如图,一次函数的图象与x轴,y轴分别相交于A,B两点,且与反比例函数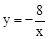 的图象在第二象限交与点C,如果点A为的坐标为(2,0),B是AC的中点.
的图象在第二象限交与点C,如果点A为的坐标为(2,0),B是AC的中点.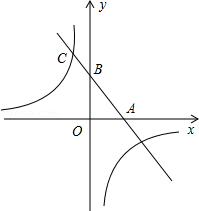
(1)求点C的坐标;
(2)求一次函数的解析式.
二次函数 的图象与 轴交于 , 两点,与 轴交于点 ,顶点为 ..
(1)求这个二次函数的表达式,并写出点 的坐标;
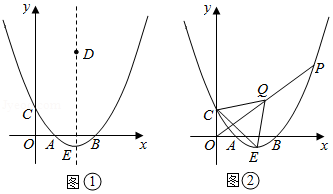
(2)如图①, 是该二次函数图象的对称轴上一个动点,当 的垂直平分线恰好经过点 时,求点 的坐标;
(3)如图②, 是该二次函数图象上的一个动点,连接 ,取 中点 ,连接 , , ,当 的面积为12时,求点 的坐标.
【感知】如图①,在四边形 中, ,点 在边 上, ,求证: .
【探究】如图②,在四边形 中, ,点 在边 上,点 在边 的延长线上, ,且 ,连接 交 于点 .
求证: .
【拓展】如图③,点 在四边形 内, 十 ,且 ,过 作 交 于点 ,若 ,延长 交 于点 .求证: .

某超市经销一种商品,每千克成本为50元,经试销发现,该种商品的每天销售量 (千克)与销售单价 (元 千克)满足一次函数关系,其每天销售单价,销售量的四组对应值如下表所示:
|
销售单价 (元 千克) |
55 |
60 |
65 |
70 |
|
销售量 (千克) |
70 |
60 |
50 |
40 |
(1)求 (千克)与 (元 千克)之间的函数表达式;
(2)为保证某天获得600元的销售利润,则该天的销售单价应定为多少?
(3)当销售单价定为多少时,才能使当天的销售利润最大?最大利润是多少?
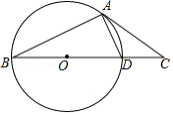
如图,在 中, 是边 上一点,以 为直径的 经过点 ,且 .
(1)请判断直线 是否是 的切线,并说明理由;
(2)若 , ,求弦 的长.
如图,在一笔直的海岸线上有 , 两个观测站, 在 的正西方向, ,从观测站 测得船 在北偏东 的方向,从观测站 测得船 在北偏西 的方向.求船 离观测站 的距离.
