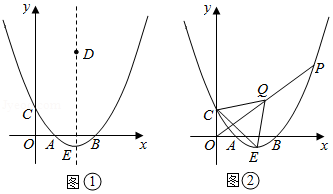
二次函数 的图象与 轴交于 , 两点,与 轴交于点 ,顶点为 ..
(1)求这个二次函数的表达式,并写出点 的坐标;
(2)如图①, 是该二次函数图象的对称轴上一个动点,当 的垂直平分线恰好经过点 时,求点 的坐标;
(3)如图②, 是该二次函数图象上的一个动点,连接 ,取 中点 ,连接 , , ,当 的面积为12时,求点 的坐标.
已知抛物线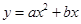 (a≠0)的顶点在直线
(a≠0)的顶点在直线 上,且过点A(4,0).
上,且过点A(4,0).
⑴求这个抛物线的解析式;
⑵设抛物线的顶点为P,是否在抛物线上存在一点B,使四边形OPAB为梯形?若存在,求出点B的坐标;若不存在,请说明理由.
⑶设点C(1,-3),请在抛物线的对称轴确定一点D,使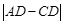 的值最大,请直接写出点D的坐标.
的值最大,请直接写出点D的坐标.
图1中所示的遮阳伞,伞柄垂直于地面,其示意图如图2.当伞收紧时,点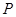 与点
与点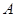 重合(此时AC=PN+CN);当伞慢慢撑开时,动点
重合(此时AC=PN+CN);当伞慢慢撑开时,动点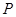 由
由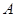 向
向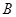 移动;当点
移动;当点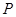 到过点
到过点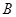 时,伞张得最开.已知伞在撑开的过程中,总有
时,伞张得最开.已知伞在撑开的过程中,总有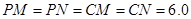 分米,
分米, 分米,
分米,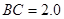 分米
分米
(1)求 长的取值范围;(2)当
长的取值范围;(2)当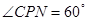 时,求
时,求 的值;
的值;
(3)在阳光垂直照射下,伞张得最开,求伞下的阴影(假定为圆面)面积为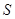 (结果保留
(结果保留 ).
).
已知“6”字形图中,FM是大⊙O的直径, BC与大⊙O相切于B, OB与小⊙O相交于A, AD∥BC,CD∥BH∥FM, DH⊥BH于H,设∠FOB=30°,OB="4," BC=6.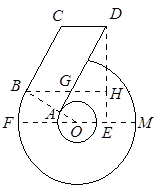
﹙1﹚求证:AD为小⊙O的切线;
﹙2﹚求DH的长.﹙结果保留根号﹚
问题背景某课外学习小组在一次学习研讨中,得到如下两个命题:
①如图1,O是正三角形ABC的中心,∠MON分别与AB、BC交于点P,Q,若∠MON = 120°,则四边形OPBQ的面积等于三角形ABC面积的三分之一.
②如图2,O是正方形ABCD的中心,∠MON分别与AB、BC交于点P,Q,若∠MON = 90°,则四边形OPBQ的面积等于正方形ABCD面积的四分之一.
然后运用类比的思想提出了如下的命题:
③如图3,O是正五边形ABCDE的中心,∠MON分别与AB、BC交于点P,Q,若∠MON = 72°,则四边形OPBQ的面积等于五边形ABCDE面积的五分之一.
任务要求
(1)请你从①、②、③三个命题中选择一个进行证明;(说明:选①做对的得5分,选②做对的得4分,选③做对的得6分)
(2)请你继续完成下面的探索:
如图④,在正n(n≥3)边形ABCDEF…中,O是中心,∠MON分别与AB、BC交于点P,Q,若∠MON等于多少度时,则四边形OPBQ的面积等于正n边形ABCDE…面积的n分之一?(不要求证明)
解:(1)我选 .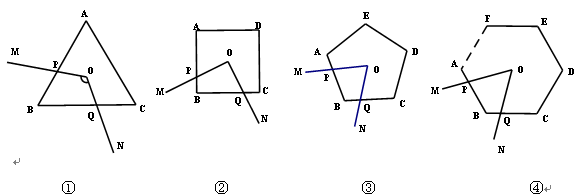
如图,一次函数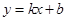 的图象与反比例函数
的图象与反比例函数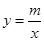 的图象相交于A、B两点.
的图象相交于A、B两点.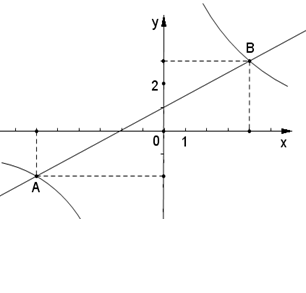
(1)根据图象,分别写出A、B的坐标;
(2)求出两函数解析式;
(3)根据图象回答:当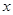 为何值时,一次函数的函数值大于反比例函数的函数值.
为何值时,一次函数的函数值大于反比例函数的函数值.