问题背景 某课外学习小组在一次学习研讨中,得到如下两个命题:
①如图1,O是正三角形ABC的中心,∠MON分别与AB、BC交于点P,Q,若∠MON = 120°,则四边形OPBQ的面积等于三角形ABC面积的三分之一.
②如图2,O是正方形ABCD的中心,∠MON分别与AB、BC交于点P,Q,若∠MON = 90°,则四边形OPBQ的面积等于正方形ABCD面积的四分之一.
然后运用类比的思想提出了如下的命题:
③如图3,O是正五边形ABCDE的中心,∠MON分别与AB、BC交于点P,Q,若∠MON = 72°,则四边形OPBQ的面积等于五边形ABCDE面积的五分之一.
任务要求
(1)请你从①、②、③三个命题中选择一个进行证明;(说明:选①做对的得5分,选②做对的得4分,选③做对的得6分)
(2)请你继续完成下面的探索:
如图④,在正n(n≥3)边形ABCDEF…中,O是中心,∠MON分别与AB、BC交于点P,Q,若∠MON等于多少度时,则四边形OPBQ的面积等于正n边形ABCDE…面积的n分之一?(不要求证明)
解:(1)我选 .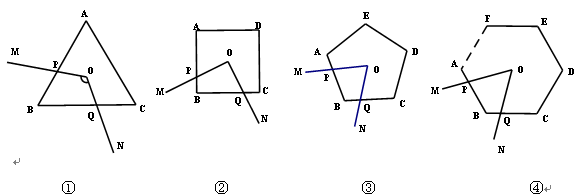
一根长60厘米的弹簧,一端固定.如果另一端挂上物体,那么在正常情况下物体的质量每增加1千克可使弹簧增长1.5厘米.
(1)正常情况下,当挂着x千克的物体时,弹簧的L长度是多少?
(2)利用(1)的结果完成下表:
| 物体的质量x(千克) |
1 |
2 |
3 |
4 |
| 弹簧的长度L(厘米) |
(3)当弹簧挂上物体后弹簧的长度为78厘米时,弹簧上挂的物体重多少千克?
已知m、n互为相反数,a、b互为倒数,x的绝对值等于2,试求代数式的值: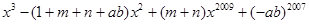 .
.
出租车司机小王某天上午营运是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天下午行车里程(单位:千米)如下:+15,-2,+5,-1,+10,-3,-2,-12,+4,-5,+6.
(1)将最后一名乘客送到目的地时,小王距下午出车时的出发点多远?
(2)若汽车耗油量为0.05升/千米,这天下午小王的汽车共耗油多少升?
化简 .
.
先化简再求值.已知:x=-2,y=3,求4x2+3xy-x2-2xy-9的值.