某超市经销一种商品,每千克成本为50元,经试销发现,该种商品的每天销售量 (千克)与销售单价 (元 千克)满足一次函数关系,其每天销售单价,销售量的四组对应值如下表所示:
销售单价 (元 千克) |
55 |
60 |
65 |
70 |
销售量 (千克) |
70 |
60 |
50 |
40 |
(1)求 (千克)与 (元 千克)之间的函数表达式;
(2)为保证某天获得600元的销售利润,则该天的销售单价应定为多少?
(3)当销售单价定为多少时,才能使当天的销售利润最大?最大利润是多少?
(本小题10分)如图,已知 、
、 是一次函数
是一次函数 的图象与反比例函数
的图象与反比例函数
的图象的两个交点.
(1)求此反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的 的取值范围.
的取值范围.
(本小题10分)一个半径为 海里的暗礁群中央
海里的暗礁群中央 处建有一个灯塔,一艘货轮由东向西航行,第一次在
处建有一个灯塔,一艘货轮由东向西航行,第一次在 处观测此灯塔在北偏西
处观测此灯塔在北偏西 方向,航行了
方向,航行了 海里后到
海里后到 ,灯塔在北偏西
,灯塔在北偏西 方向,如图.问货轮沿原方向航行有无危险?
方向,如图.问货轮沿原方向航行有无危险?
(本小题10分)如图,已知在 中,
中, 是
是 平分线,点
平分线,点 在
在 边上,且
边上,且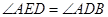 .
.
求证:(1)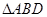 ∽
∽ ;(2)
;(2) .
.
在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球,它们除颜色外完全相同,其
中红球有2个,黄球有1个,蓝球有1个.现有一张电影票,小明和小亮决定通过摸球游戏定输赢(赢的
一方得电影票).游戏规则是:两人各摸1次球,先由小明从纸箱里随机摸出1个球,记录颜色后放回,
将小球摇匀,再由小亮随机摸出1个球并记录颜色.若两人摸到的球颜色相同,则小明赢,否则小亮赢.这
个游戏规则对双方公平吗?请你利用树状图或列表法说明理由.
已知:如图,抛物线y=ax2+bx+2与x轴的交点是A(3,0)、B(6,0),与y轴的交点是C.
(1)求抛物线的函数表达式;
(2)设P(x,y)(0<x<6)是抛物线上的动点,过点P作PQ∥y轴交直线BC于点Q.
①当x取何值时,线段PQ的长度取得最大值,其最大值是多少?
②是否存在这样的点P,使△OAQ为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.