在兰州市开展的“体育、艺术2+1”活动中,某校根据实际情况,决定主要开设A:乒
乓球,B:篮球,C:跑步,D:跳绳这四种运动项目.为了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,
并将调查结果绘制成如下的条形统计图和扇形统计图.请你结合图中信息解答下列问题: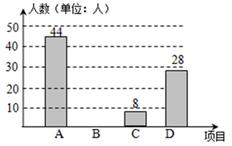
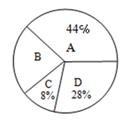
(1)样本中喜欢B项目的人数百分比是 ,其所在扇形统计图中的圆心角的度数是 ;
(2)把条形统计图补充完整;
(3)已知该校有1000人,根据样本估计全校喜欢乒乓球的人数是多少?
已知反比例函数 的图象分别位于第二、第四象限,化简: .
如图, , , .求 的度数.
解不等式组: .
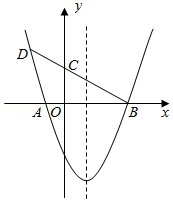
如图,抛物线 与 轴交于 , 两点,点 , 分别位于原点的左、右两侧, ,过点 的直线与 轴正半轴和抛物线的交点分别为 , , .
(1)求 , 的值;
(2)求直线 的函数解析式;
(3)点 在抛物线的对称轴上且在 轴下方,点 在射线 上.当 与 相似时,请直接写出所有满足条件的点 的坐标.
如图,点 是反比例函数 图象上一点,过点 分别向坐标轴作垂线,垂足为 , .反比例函数 的图象经过 的中点 ,与 , 分别相交于点 , .连接 并延长交 轴于点 ,点 与点 关于点 对称,连接 , .
(1)填空: ;
(2)求 的面积;
(3)求证:四边形 为平行四边形.
