在平面直角坐标系中,已知抛物线 (b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.
(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.
(1)如图,若该抛物线过A,B两点,求该抛物线的函数表达式;
(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与AC交于另一点Q.
(i)若点M在直线AC下方,且为平移前(1)中的抛物线上的点,当以M、P、Q三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点M的坐标;
(ii)取BC的中点N,连接NP,BQ.试探究 是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
如图,平面直角坐标系中,直线AB:y=-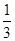 x+b交y轴于点A(0,1),交x轴于点B.直线x=1交AB于点D,交x轴于点E,P是直线x=1上一动点,且在点D的上方,设P(1,n).
x+b交y轴于点A(0,1),交x轴于点B.直线x=1交AB于点D,交x轴于点E,P是直线x=1上一动点,且在点D的上方,设P(1,n).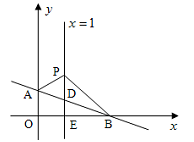
(1)求直线AB的解析式和点B的坐标;
(2)求△ABP的面积(用含n的代数式表示);
(3)当S△ABP=2时,以PB为边在第一象限作等腰直角三角形BPC,求出点C的坐标.(考虑问题要全面哦……)
我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你学过的特殊四边形中是勾股四边形的两种图形的名称,;
(2)如图(1),已知格点(小正方形的顶点)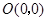 ,
,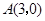 ,
,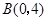 ,请你画出以格点为顶点,
,请你画出以格点为顶点,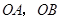 为勾股边且对角线相等的非长方形的勾股四边形
为勾股边且对角线相等的非长方形的勾股四边形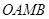 ;并写出点M的坐标.
;并写出点M的坐标.
(3)如图(2),将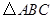 绕顶点
绕顶点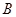 按顺时针方向旋转
按顺时针方向旋转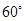 ,得到
,得到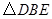 ,连结
,连结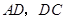 ,已知
,已知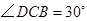 .求证:
.求证: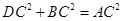 ,即四边形
,即四边形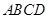 是勾股四边形.
是勾股四边形.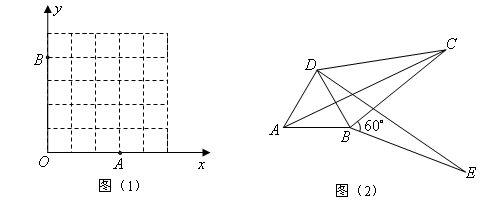
细心观察下列图形,认真分析各式,然后解答问题:s1,s2, s3,…表示各个三角形的面积
OA22=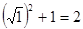
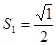 ;
;
OA32=12+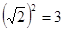
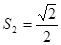 ;
;
OA42=12+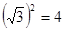
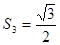
…………
(1)推算出OA10的长.
(2) 请用含有n(n是正整数)的等式表示上述的两个变化规律.
(3)若一个三角形的面积是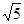 ,通过计算说明它是第几个三角形?
,通过计算说明它是第几个三角形?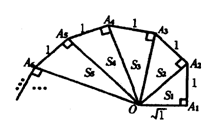
已知在平面直角坐标系中有三点A(-2,1)、B(3,1)、C(2,3).请回答如下问题:
(1)在坐标系内描出点A、B、C的位置;
(2)在平面直角坐标系中画出△A′B′C′,使它与△ABC 关于x轴对称,并写出顶点C’的坐标.
(3)若M(x,y)是△ABC内部任意一点,请直接写出这点在△A′B′C′内部的对应点M'的坐标.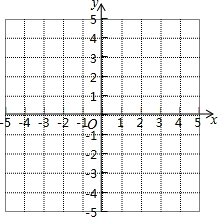
如图,一次函数y=kx+b的图象经过A、B两点,与x轴交于点C,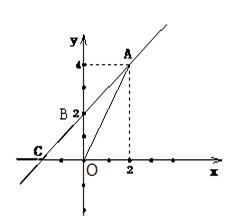
(1)求此一次函数的解析
(2)求△AOC的面积.