如图，抛物线
（a≠0）交x轴于A、B两点，A点坐标为（3，0），与y轴交于点C（0，4），以OC、OA为边作矩形OADC交抛物线于点G．
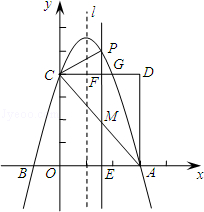
（1）求抛物线的解析式；
（2）抛物线的对称轴l在边OA（不包括O、A两点）上平行移动，分别交x轴于点E，交CD于点F，交AC于点M，交抛物线于点P，若点M的横坐标为m，请用含m的代数式表示PM的长；
（3）在（2）的条件下，连结PC，则在CD上方的抛物线部分是否存在这样的点P，使得以P、C、F为顶点的三角形和△AEM相似？若存在，求出此时m的值，并直接判断△PCM的形状；若不存在，请说明理由。
完成y=
的图象,并根据图象回答问题.
(1)根据图象指出,当y=-2时x的值;
(2)根据图象指出,当-2<x<1时,y的取值范围;
(3)根据图象指出,当-3<y<2时,x的取值范围.
已知y=y1-y2,其中y1是x的反比例函数,y2是x2的正比例函数,且x=1时y=3,x=-2时y=-15.
求:(1)y与x之间的函数关系式;
(2)当x=2时y的值.
如图,是一辆小汽车沿一条高速公路匀速前进的时间t(小时)与速度x(千米/时)关系的图象,根据图象提供的信息回答下列问题: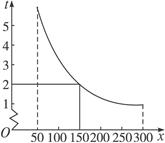
(1)这条高速公路的全长是多少千米?
(2)写出速度与时间之间的函数关系.
(3)汽车最大速度可以达到多少?
(4)汽车最慢用几个小时可以到达?如果要在3小时以内到达,汽车的速度应不少于多少?
反比例函数y=
的图象经过点A(4,-2),
(1)求这个函数的解析式;
(2)请判断点B(1,8)是否在这个反比例函数的图象上,并说明理由.
△ABC是锐角三角形，BC=6，面积为12.点P在AB上，点Q在AC上.如图9-33，正方形PQRS（RS与A在PQ的异侧）的边长为x，正方形PQRS与△ABC的公共部分的面积为y.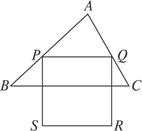
（1）当RS落在BC上时，求x；
（2）当RS不落在BC上时，求y与x的函数关系式；
（3）求公共部分面积的最大值.