随着车辆的增加,交通违规的现象越来越严重,交警对某雷达测速区检测到的一组汽车的时速数据进行整理,得到其频数及频率如表(未完成):
| 数据段 |
频数 |
频率 |
| 30~40 |
10 |
0.05 |
| 40~50 |
36 |
|
| 50~60 |
|
0.39 |
| 60~70 |
|
|
| 70~80 |
20 |
0.10 |
| 总计 |
200 |
1 |
注:30~40为时速大于等于30千米而小于40千米,其他类同
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;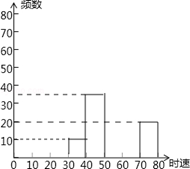
(3)如果汽车时速不低于60千米即为违章,则违章车辆共有多少辆?
(本题8分)阅读下面材料,再回答问题:
有一些几何图形可以被某条直线分成面积相等的两部分,我们将“把一个几何图形分成面积相等的两部分的直线叫做该图形的二分线”,如:圆的直径所在的直线是圆的“二分线”,正方形的对角线所在的直线是正方形的“二分线”.
解决下列问题:
(1)菱形的“二分线”是;
(2)三角形的“二分线”是;
(3)在下图中,试用两种不同的方法分别画出等腰梯形ABCD的“二分线”,简述做法.

图1图2
(本题7分)小明本学期的数学成绩如下表所示:
| 测验类别 |
平时 |
a |
b |
c |
|||
| 测试1 |
测试2 |
测试3 |
测试4 |
平时平均数 |
期中考试 |
期末考试 |
|
| 成绩 |
108 |
103 |
101 |
108 |
110 |
114 |
(1)六次考试的中位数和众数分别是什么?
(2)请计算小明该学期的数学平时平均成绩;
(3)如果学期的总评成绩是根据如图所示的比例计算所得,已知小明该学期的数学总评成绩为111分,请计算出总评成绩中期中、期末成绩各自所占的比例.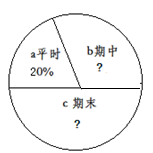
(本题7分) 如图,四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE =CF.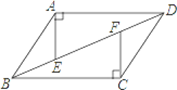
求证:(1)△ADE ≌△CBF;
(2)AB=CD.
(每小题4分,共8分)计算:
(1)已知:(x+2)2=25,求x;
(2)计算: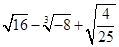 .
.
如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE,等边△BCF。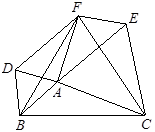
(1)求证:四边形DAEF平行四边形;
(2)(2)探究下列问题:(只填满足的条件,不需要证明)
①当∠A=时,四边形DAEF是矩形;
②当△ABC满足条件时,四边形DAEF是菱形;
③当△ABC满足条件时;以D、A、E、F为顶点的四边形不存在