如图1,点A是x轴正半轴上的动点,点B的坐标为(0,4),M是线段AB的中点。将点M绕点A顺时针方向旋转900得到点C,过点C作x轴的垂线,垂足为F,过点B作y轴的垂线与直线CF相交于点E,点D是点A关于直线CF的对称点。连结AC,BC,CD,设点A的横坐标为t,
(1)当t=2时,求CF的长;
(2)①当t为何值时,点C落在线段CD上;
②设△BCE的面积为S,求S与t之间的函数关系式;
(3)如图2,当点C与点E重合时,将△CDF沿x轴左右平移得到 ,再将A,B,
,再将A,B, 为顶点的四边形沿
为顶点的四边形沿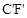 剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形。请直接写出符合上述条件的点
剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形。请直接写出符合上述条件的点 坐标,
坐标,
已知函数y=-4x2-2mx+m2与反比例函数y=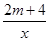 的图象在第二象限内的一个交点的横坐标是-2,求此两个函数的解析式.
的图象在第二象限内的一个交点的横坐标是-2,求此两个函数的解析式.
如图,在平面直角坐标系xOy中,二次函数图象的顶点坐标为C(-4,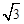 ),且在x轴上截得的线段AB的长为6.
),且在x轴上截得的线段AB的长为6.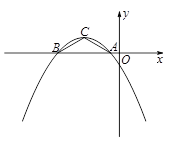
(1)求二次函数的解析式;
(2)在y轴上确定一点M,使MA+MC的值最小,求出点M的坐标;
(3)在x轴下方的抛物线上,是否存在点N,使得以N、A、B三点为顶点的三角形与△ABC相似?如果存在,求出点N的坐标;如果不存在,请说明理由.
如图,菱形ABCD的边长为48cm,∠A=60°,动点P从点A出发,沿着线路AB—BD做匀速运动,动点Q从点D同时出发,沿着线路DC—CB—BA做匀速运动.
(1)求BD的长;
(2)已知动点P、Q运动的速度分别为8cm/s、10cm/s. 经过12秒后,P、Q分别到达M、N两点,若按角的大小进行分类,请问△AMN是哪一类三角形,并说明理由;
(3)设问题(2)中的动点P、Q分别从M、N同时沿原路返回,动点P的速度不变,动点Q的速度改变为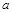 cm/s,经过3秒后,P、Q分别到达E、F两点,若△BEF与问题(2)中的△AMN相似,试求
cm/s,经过3秒后,P、Q分别到达E、F两点,若△BEF与问题(2)中的△AMN相似,试求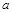 的值.
的值.
如图,小明在一次高尔夫球训练中,从山坡下P点打出一球向球洞A点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大高度BD为12米时,球移动的水平距离PD为9米 .已知山坡PA与水平方向PC的夹角为30o,AC⊥PC于点C, P、A两点相距 米.请你建立适当的平面直角坐标系解决下列问题.
米.请你建立适当的平面直角坐标系解决下列问题. 
(1)求水平距离PC的长;
(2)求出球的飞行路线所在抛物线的解析式;
(3)判断小明这一杆能否把高尔夫球从P点直接打入球洞A.
阅读下面材料:
小伟遇到这样一个问题:如图1,在正三角形ABC内有一点P,且PA="3" ,PB=4,PC=5,求∠APB的度数.
小伟是这样思考的:如图2,利用旋转和全等的知识构造△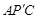 ,连接
,连接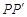 ,得到两个特殊的三角形,从而将问题解决.
,得到两个特殊的三角形,从而将问题解决.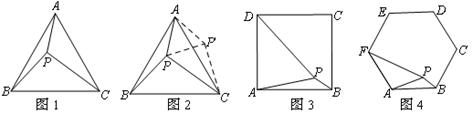
请你回答:图1中∠APB的度数等于 .
参考小伟同学思考问题的方法,解决下列问题:
(1)如图3,在正方形ABCD内有一点P,且PA= ,PB=1,PD=
,PB=1,PD=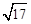 ,则∠APB的度数等于,正方形的边长为;
,则∠APB的度数等于,正方形的边长为;
(2)如图4,在正六边形ABCDEF内有一点P,且PA=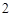 ,PB=1,PF=
,PB=1,PF= ,则∠APB的度数等于,正六边形的边长为.
,则∠APB的度数等于,正六边形的边长为.