如图,在平面直角坐标系中,二次函数 的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.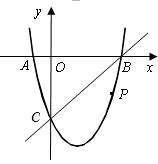
(1)求二次函数解析式;
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形 .是否存在点P,使四边形
.是否存在点P,使四边形 为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
(年内蒙古包头、乌兰察布12分)如图,已知∠MON=90°,A是∠MON内部的一点,过点A作AB⊥ON,垂足为点B,AB=3厘米,OB=4厘米,动点E,F同时从O点出发,点E以1.5厘米/秒的速度沿ON方向运动,点F以2厘米/秒的速度沿OM方向运动,EF与OA交于点C,连接AE,当点E到达点B时,点F随之停止运动.设运动时间为t秒(t>0).
(1)当t=1秒时,△EOF与△ABO是否相似?请说明理由;
(2)在运动过程中,不论t取何值时,总有EF⊥OA.为什么?
(3)连接AF,在运动过程中,是否存在某一时刻t,使得S△AEF= S四边形ABOF?若存在,请求出此时t的值;若不存在,请说明理由.
S四边形ABOF?若存在,请求出此时t的值;若不存在,请说明理由.
(2014年江苏镇江9分)如图1,在平面直角坐标系xOy中,点M为抛物线 的顶点,过点(0,4)作x轴的平行线,交抛物线于点P、Q(点P在Q的左侧),PQ=4.
的顶点,过点(0,4)作x轴的平行线,交抛物线于点P、Q(点P在Q的左侧),PQ=4.
(1)求抛物线的函数关系式,并写出点P的坐标;
(2)小丽发现:将抛物线 绕着点P旋转180°,所得新抛物线的顶点恰为坐标原点O,你认为正确吗?请说明理由;
绕着点P旋转180°,所得新抛物线的顶点恰为坐标原点O,你认为正确吗?请说明理由;
(3)如图2,已知点A(1,0),以PA为边作矩形PABC(点P、A、B、C按顺时针的方向排列), .
.
①写出C点的坐标:C( , )(坐标用含有t的代数式表示);
②若点C在题(2)中旋转后的新抛物线上,求t的值.
(年湖南长沙10分)如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的对称轴为y轴,且经过(0,0)和( )两点,点P在该抛物线上运动,以点P为圆心的⊙P总经过定点A(0,2).
)两点,点P在该抛物线上运动,以点P为圆心的⊙P总经过定点A(0,2).
(1)求a,b,c的值;
(2)求证:在点P运动的过程中,⊙P始终与x轴相交;
(3)设⊙P与x轴相交于M(x1,0),N(x2,0)(x1<x2)两点,当△AMN为等腰三角形时,求圆心P的纵坐标.
(年甘肃白银、定西、平凉、酒泉、临夏12分)如图,在平面直角坐标系xOy中,顶点为M的抛物线是由抛物线y=x2﹣3向右平移一个单位后得到的,它与y轴负半轴交于点A,点B在该抛物线上,且横坐标为3.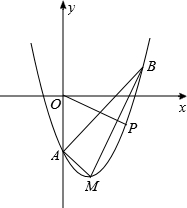
(1)求点M、A、B坐标;
(2)连结AB、AM、BM,求∠ABM的正切值;
(3)点P是顶点为M的抛物线上一点,且位于对称轴的右侧,设PO与x正半轴的夹角为α,当α=∠ABM时,求P点坐标.
(年四川南充8分)如图,已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的延长线上,EP=EG,
(1)求证:直线EP为⊙O的切线;
(2)点P在劣弧AC上运动,其他条件不变,若BG2=BF•BO.试证明BG=PG;
(3)在满足(2)的条件下,已知⊙O的半径为3,sinB= .求弦CD的长.
.求弦CD的长.