如图，在△ABC中，AB=AC，D是BA延长线上的一点，点E是AC的中点。
（1）实践与操作：利用尺规按下列要求作图，并在图中标明相应字母（保留作图痕迹，不写作法）。
①作∠DAC的平分线AM。②连接BE并延长交AM于点F。
（2）猜想与证明：试猜想AF与BC有怎样的位置关系和数量关系，并说明理由。
如图，在
ABCD中，∠DAB=60°，AB=2AD，点E、F分别是AB、CD的中点，过点A作AG∥BD，交CB的延长线于点G。
（1）求证：四边形DEBF是菱形；
（2）请判断四边形AGBD是什么特殊四边形？并加以证明。
某商场销售一种进价为20元／台的台灯，经调查发现，该台灯每天的销售量w(太)与销售单价x(元)满足
，设销售这种台灯每天的利润为y（元）。
（1）求y与x之间的函数关系式；
（2）当销售单价定为多少元时．每天的利润最大？最大利润是多少？
（3）在保证销售量尽可能大的前提下．该商场每天还想获得150元的利润．应将销售单价定为多少元？
如入，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于点E，AD⊥CE于点D。
求证：△BEC≌△CDA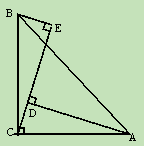
解方程：
如图，∠C=90°，点A、B在∠C的两边上，CA=30，CB=20，连结AB．点P从
点B出发，以每秒4个单位长度的速度沿BC方向运动，到点C停止．当点P与B、C
两点不重合时，作PD⊥BC交AB于D，作DE⊥AC于E．F为射线CB上一点，且∠CEF=∠ABC．设
点P的运动时间为x（秒）．
（1）用含有x的代数式表示CF的长．
（2）求点F与点B重合时x的值．
（3）当点F在线段CB上时，设四边形DECP与四边形DEFB重叠部分图形的面积为y（平方单位）．求y与x之间的函数关系式．
（4）当x为某个值时，沿PD将以D、E、F、B为顶点的四边形剪开，得到两个图形，用这两个图形拼成不重叠且无缝隙的图形恰好是三角形．请直接写出所有符合上述条件的x值．