已知以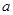 为首项的数列
为首项的数列 满足:
满足: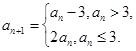
(1)若 ,求证:
,求证: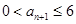 ;
;
(2)若 ,求使
,求使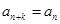 对任意正整数n都成立的
对任意正整数n都成立的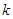 与
与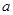 .
.
第一小题3分,第二小题5分,第三小题6分.
(1) 已知函数 是奇函数(
是奇函数( 为常数),求实数
为常数),求实数 的值;
的值;
(2)若 ,且
,且 ,求
,求 的解析式;
的解析式;
(3)对于(2)中的 ,若
,若 有正数解,求实数
有正数解,求实数 的取值范围。
的取值范围。
如图,正四棱柱 的底面边长为1,异面直线
的底面边长为1,异面直线 与
与 所成角的大小为
所成角的大小为 ,求:
,求:
(1)线段
 到底面
到底面 的距离;
的距离;
(2)三棱椎 的体积。
的体积。
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
(1)数列 各项均不为0,前n项和为
各项均不为0,前n项和为 ,
, ,
, 的前n项和为
的前n项和为 ,且
,且 ,若数列
,若数列 共3项,求所有满足要求的数列;
共3项,求所有满足要求的数列;
(2)求证: 是满足已知条件的一个数列;
是满足已知条件的一个数列;
(3)请构造出一个满足已知条件的无穷数列 ,并使得
,并使得 ;若还能构造其他符合要求的数列,请一并写出(不超过四个)。
;若还能构造其他符合要求的数列,请一并写出(不超过四个)。
本题共有3个小题,第一小题3分,第二小题7分,第三小题6分
如图,曲线 由曲线
由曲线 和曲线
和曲线 组成,其中点
组成,其中点 为曲线
为曲线 所在圆锥曲线的焦点,点
所在圆锥曲线的焦点,点 为曲线
为曲线 所在圆锥曲线的焦点,
所在圆锥曲线的焦点,
(1)若 ,求曲线
,求曲线 的方程;
的方程;
(2)如图,作直线 平行于曲线
平行于曲线 的渐近线,交曲线
的渐近线,交曲线 于点A、B,求证:弦AB的中点M必在曲线
于点A、B,求证:弦AB的中点M必在曲线 的另一条渐近线上;
的另一条渐近线上;
(3)对于(1)中的曲线 ,若直线
,若直线 过点
过点 交曲线
交曲线 于点C、D,求
于点C、D,求 面积的最大值。
面积的最大值。
第一小题3分,第二小题5分,第三小题6分.
(1)已知函数 是奇函数,
是奇函数, 为常数,求实数
为常数,求实数 的值;
的值;
(2)若 ,且
,且 ,求
,求 的解析式;
的解析式;
(3)对于(2)中的 ,若
,若 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.