仔细阅读下面问题的解法:
设A=[0,1],若不等式21-x+a>0在A上有解,求实数a的取值范围.
解:令f(x)=21-x+a,因为f(x)>0在A上有解。
=2+a>0 a>-2
a>-2
学习以上问题的解法,解决下面的问题,已知:函数f(x)=x2+2x+3(-2≤x≤-1).
①求f(x)的反函数f-1(x)及反函数的定义域A;
②设B= ,若A∩B≠
,若A∩B≠ ,求实数a的取值范围.
,求实数a的取值范围.
成都市海关对同时从A,B,C三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如表所示.工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测.
| 地区 |
A |
B |
C |
| 数量 |
50 |
150 |
100 |
(1)求这6件样品中来自A,B,C各地区商品的数量;
(2)若在这6件样品中随机抽取2件送往甲机构进行进一步检测,求这2件商品中来自C地区的样品数X的分布列及数学期望。
本小题满分12分)已知函数 ,
, 三个内角
三个内角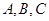 的对边分别为
的对边分别为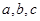 .
.
(Ⅰ)求 的单调递增区间及对称轴的方程;
的单调递增区间及对称轴的方程;
(Ⅱ)若 ,
,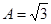
 ,求角
,求角 的大小.
的大小.
(本小题满分14分)已知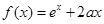 (
( 为常数),曲线
为常数),曲线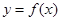 在点
在点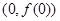 处的切线与直线
处的切线与直线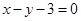 垂直.
垂直.
(Ⅰ)求 的值及函数
的值及函数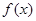 的单调区间;
的单调区间;
(Ⅱ)证明:当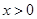 时,
时, ;
;
(Ⅲ)设 ,若
,若 在
在 上单调递减,求实数
上单调递减,求实数 的取值范围.
的取值范围.
(本小题满分13分)
等差数列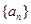 的前
的前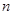 项和为
项和为 ,已知
,已知 为整数,且在前
为整数,且在前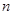 项和中
项和中 最大.
最大.
(Ⅰ)求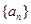 的通项公式;
的通项公式;
(Ⅱ)设 .
.
(1)求证: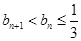 ;(2)求数列
;(2)求数列 的前
的前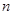 项和
项和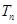 .
.
(本小题满分12分) 已知函数 满足
满足 ,对任意
,对任意 ,都有
,都有 ,且
,且 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若 ,使方程
,使方程 成立,求实数
成立,求实数 的取值范围.
的取值范围.