已知二次函数h(x)=ax2+bx+c(其中c<3)，其导函数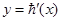
的图象如图，f(x)=6lnx+h(x).
①求f(x)在x=3处的切线斜率；
②若f(x)在区间(m,m+
)上是单调函数，求实数m的取值范围；
③若对任意k∈[-1,1]，函数y=kx(x∈(0,6])的图象总在函数y＝f(x)图象的上方，求c的取值范围.
如图，在某城市中，Ｍ，Ｎ两地之间有整齐的方格形道路网，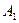
、
、
、
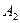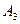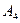是道路网中位于一条对角线上的４个交汇处，今在道路网Ｍ、Ｎ处的甲、乙两人分别要到Ｍ，Ｎ处，他们分别随机地选择一条沿街的最短路径，同时以每１０分钟一格的速度分别向Ｎ，Ｍ处行走，直到到达Ｎ，Ｍ为止。
（１）求甲经过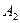的概率；
（２）求甲、乙两人相遇经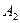点的概率；
（３）求甲、乙两人相遇的概率；
旅游公司为3个旅游团提供4条旅游线路，每个旅游团任选其中一条. 
（1）求3个旅游团选择3条不同的线路的概率
（2）求恰有2条线路没有被选择的概率.
（3）求选择甲线路旅游团数的期望.
一纸箱中装有大小相等，但已编有不同号码的白色和黄色乒乓球，其中白色乒乓球有6个，黄色乒乓球有2个。
（Ⅰ）从中任取2个乒乓球，求恰好取得1个黄色乒乓球的概率；
（Ⅱ）每次不放回地抽取一个乒乓球，求第一次取得白色乒乓球时已取出的黄色乒乓球个数ξ的分布列及数学期望Eξ。
已知暗箱中开始有3个红球，2个白裘。现每次从暗箱中取出一个球后，再将此球以及与它同色的5个球（共6个球）一起放回箱中。
(1)求第二次取出红球的概率；
(2)求第三次取出白球的概率；
(3)设取出白球得5分，取出红球得8分，求连续取球3次得分的期望值。
盒内有大小相同的9个球，其中2个红色球，3个白色球，4个黑色球. 规定取出1个红色球得1分，取出1个白色球得0分，取出1个黑色球得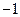
分 . 现从盒内任取3个球.
（Ⅰ）求取出的3个球颜色互不相同的概率；
（Ⅱ）求取出的3个球得分之和恰为1分的概率；
（Ⅲ）设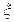
为取出的3个球中白色球的个数，求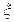的分布列和数学期望.