已知幂函数
的图象与x轴，y轴无交点且关于原点对称，又有函数f(x)=x2－alnx+m－2在(1，2]上是增函数，g(x)=x－
在(0,1)上为减函数.
①求a的值；
②若
，数列{an}满足a1＝1，an+1＝p(an)，（n∈N+），数列{bn}，满足
，
，求数列{an}的通项公式an和sn.
③设
，试比较[h(x)]n+2与h(xn)+2n的大小（n∈N+），并说明理由.
(本题满分12分)已知数列{an}的前n项和为Sn，且an=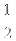
(3n+Sn)对一切正整数n成立
（1）证明：数列{3+an}是等比数列，并求出数列{an}的通项公式；
（2）设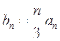
，求数列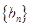
的前n项和Bn；
(本题满分12分)已知命题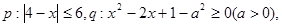
若非
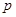是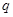
的充分不必要条件，求
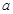的取值范围。
(本题满分10分)已知集合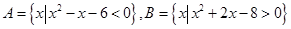
，求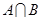
.
.如图，直三棱柱ABC-A1B1C1中，AB⊥AC, D、E分别为AA1、B1C的中点，DE⊥平面BCC1
（Ⅰ）证明：AB=AC;
（Ⅱ）设二面角A-BD-C为60°,求B1C与平面BCD所成的角的大小.
已知
的内接△ABC中，点A的坐标是(－3,0)，重心G的坐标是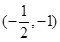
，求：(1)直线BC的方程;(2)弦BC的
长度.