如图,在平面直角坐标系 中,
中, 、
、 分别是椭圆
分别是椭圆 的顶点,过坐标原点的直线交椭圆于
的顶点,过坐标原点的直线交椭圆于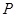 、
、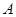 两点,其中
两点,其中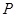 在第一象限.过
在第一象限.过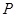 作
作 轴的垂线,垂足为
轴的垂线,垂足为 .连接
.连接 ,并延长交椭圆于点
,并延长交椭圆于点 .设直线
.设直线 的斜率为
的斜率为 .
.
(Ⅰ)当直线 平分线段
平分线段 时,求
时,求 的值;
的值;
(Ⅱ)当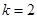 时,求点
时,求点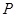 到直线
到直线 的距离;
的距离;
(Ⅲ)对任意 ,求证:
,求证: .
.
(.在一次购物抽奖活动中,假设某10张券中有一等奖奖券1张,可获价值50元的奖品;有二等奖奖券3张,每张可获价值10元的奖品;其余6张没奖。某顾客从此10张奖券中任抽2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值X(元)的概率分布列。
求以下问题的排列数:
(1)4男3女排成一排,3女相邻。
(2)4男3女排成一排 ,女不能排在两端。
,女不能排在两端。
(3)4男3女排成一排,男女相间。(结果用数字表示)
甲、乙两人各进行3次射击,甲每次击中目标的概率为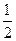 ,乙每次击中目标的概率为
,乙每次击中目标的概率为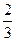 .
.
(1)记甲击中目标的次数为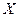 ,求
,求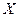 的概率分布列及数学期望EX;
的概率分布列及数学期望EX;
(2)求甲恰好比乙多击中目标2次的概率.
(14分) 已知函数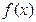 定义域为
定义域为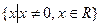 ,对于定义域内的任意x,y都有
,对于定义域内的任意x,y都有 ,且
,且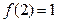 ,当
,当
(13分) 已知函数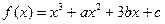
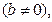 且
且 是奇
是奇 函数.
函数.
(1) 求 的值; (2) 求函数
的值; (2) 求函数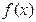 的单调区间.
的单调区间.