在直角坐标系 中,以
中,以 为极点,
为极点,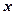 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 ,
, 分别为曲线
分别为曲线 与
与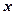 轴,
轴, 轴的交点.
轴的交点.
(1)写出曲线 的直角坐标方程,并求出
的直角坐标方程,并求出 的极坐标;
的极坐标;
(2)设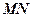 的中点为
的中点为 ,求直线
,求直线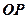 的极坐标方程.
的极坐标方程.
袋子A和袋子B均装有红球和白球,从A中摸出一个红球的概率是 ,从B中摸出一个红球的概率是P.
,从B中摸出一个红球的概率是P.
(1)从A中有放回地摸球,每次摸出一个,共摸5次,求恰好有3次摸到红球的概率;
(2)若A、B两个袋子中的总球数之比为1:2,将A、B中的球装在一起后,从中摸出一个红球的概率为 ,求P的值.
,求P的值.
某热水瓶胆生产的6件产品中,有4件正品,2件次品,正品和次品在外观上没有区别,从这6件产品中任意抽检2件,计算
(1)2件都是正品的概率
(2)至少有一件次品的概率.
甲有一个箱子,里面放有x个红球,y个白球(x,y≥0,且x+y=4);乙有一个箱子,里面放有2个红球,1个白球,1个黄球.现在甲从箱子任取2个球,乙从箱子里在取1个球,若取出的3个球颜色全不相同,则甲获胜.
(1)试问甲如何安排箱子里两种颜色的个数,才能使自己获胜的概率最大?
(2)在(1)的条件下,求取出的3个球中红球个数的数学期望.
已知10件不同的产品中共有3件次品,现对它们进行一一测试,直到找出所有3件次品为止.
(1)求恰好在第5次测试时3件次品全部被测出的概率;
(2)记恰好在第k次测试时3件次品全部被测出的概率为f(k),求f(k)的最大值和最小值.
甲与乙两人掷硬币,甲用一枚硬币掷3次,记下国徽面朝上的次数为m;乙用一枚硬币掷2次,记下国徽面朝上的次数为n.
(1)算国徽面朝上不同次数的概率并填入下表:
(2)现规定:若m>n,则甲胜;若n≥m,则乙胜.你认为这种规定合理吗?为什么?